This post summarises my responses to a question at Eng-Tips.

The UK concrete standard in use before Eurocode 2 (BS 8110) has a simple procedure for designing columns subject to bending about both principal axes:

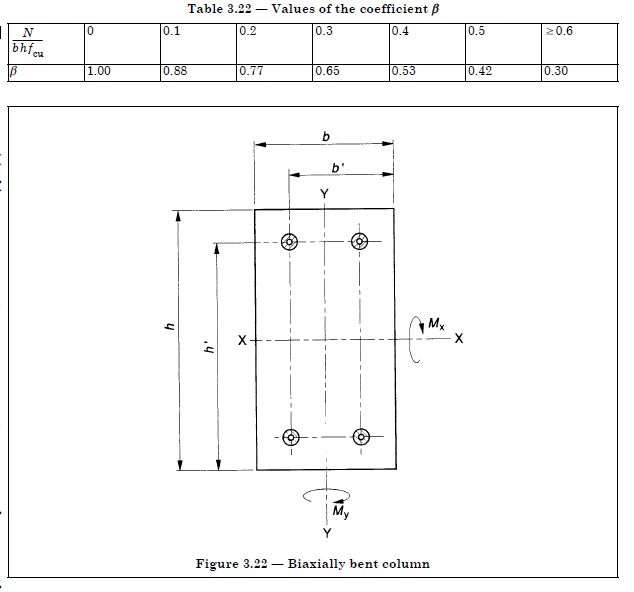
This allows the column to be designed to resist a factored moment about one axis.

Eurocode 2 has a different approach:

AS 3600 follows the same approach as Eurocode 2, but with slightly different exponent factors:

The Eurocode/AS 3600 procedure requires the section capacity to be checked about both axes, but it’s actually quite easy to derive an equation for the minimum resistance moment for the axis with the larger moment, similar to the BS8110 one:

For applied moment Me and moment resistance Mr, if Me/Mr is equal about the two axes then Equation 5.39 reduces to:

2(Me/Mr)^a <= 1.0

So for minimum Mr: (Me/Mr)^a = 0.5

Me/Mr = 0.5^(1/a)

Mr = Me/(0.5^(1/a))

In the graph below I have plotted 1/(0.5^(1/a)) with 1 + Beta from BS8110, the equivalent factor from the Australian code (AS 3600), and the factor derived from the biaxial analysis of a square section with equal moments about both axes, for a range of axial loads:

The factor is applied to the design bending moment, so a higher factor is more conservative.

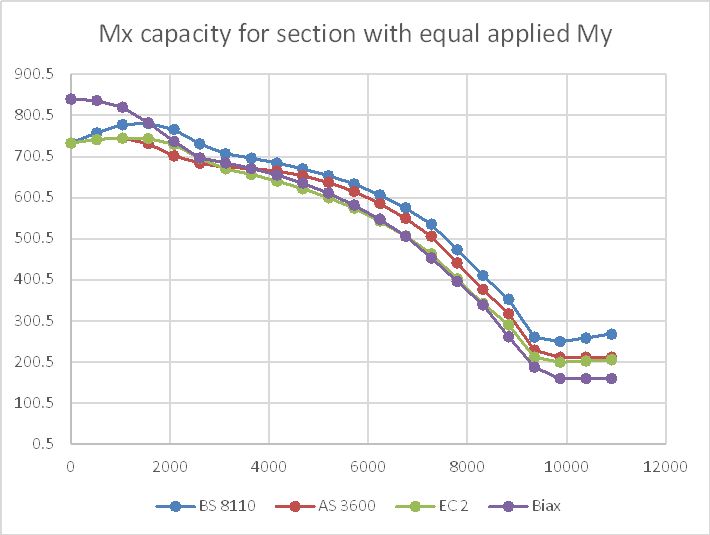
The graph below shows the ULS bending capacity about one axis for a square section with equal applied moment about both axes. The section details were:

• Dimensions: 600 x 600
• Reinforcement; 4 N20 bars each face, yield strength = 500 MPa
• Concrete: 40 MPa, cover 40 mm

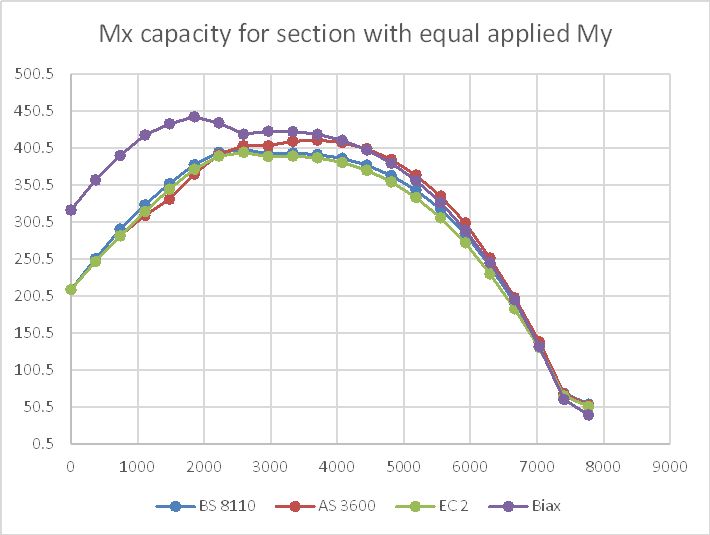
Increasing the steel diameter to 40 mm has a significant effect on the results, with the simplified methods being much less conservative under high axial loads, and very unconservative under very high axial loads: