Further to the previous post the py_UMom spreadsheet has now been updated for the latest Python and Numpy versions. The latest version can be downloaded from:

py_UMom.zip

In addition to the Python code changes, the example of the OptShearCap3600 function has been updated to use the option to limit the force in the vertical shear steel when checking longitudinal forces due to shear to the current AS 5100.5 code (see Longitudinal force due to shear for details).

Examples of this function are shown below, comparing AS 3600 (with and without adjustment of the compression strut angle) with AS 5100.5 (with and without a limit applied to the value of Vus). In the first examples the reduction factors for bending and shear have been adjusted in the AS 3600 results so that the only difference between the two codes is in the treatment of longitudinal loads due to shear.

With 12 mm shear steel at 200 spacing all results are equal where shear controls the section design but for higher moments the first AS 3600 results are more conservative. If the strut angle is adjusted AS 3600 has a slightly higher capacity than the AS 5100.5 results, where the two options are almost equal up to a moment of about 375 kNm. For higher moments the AS 5100.5 results give a higher capacity, but these values are un-conservative because they use a force in the shear steel greater than the applied shear force. Applying a limit to this force, the AS 5100.5 results are very close to the AS 3600 results with adjustment of the strut angle:

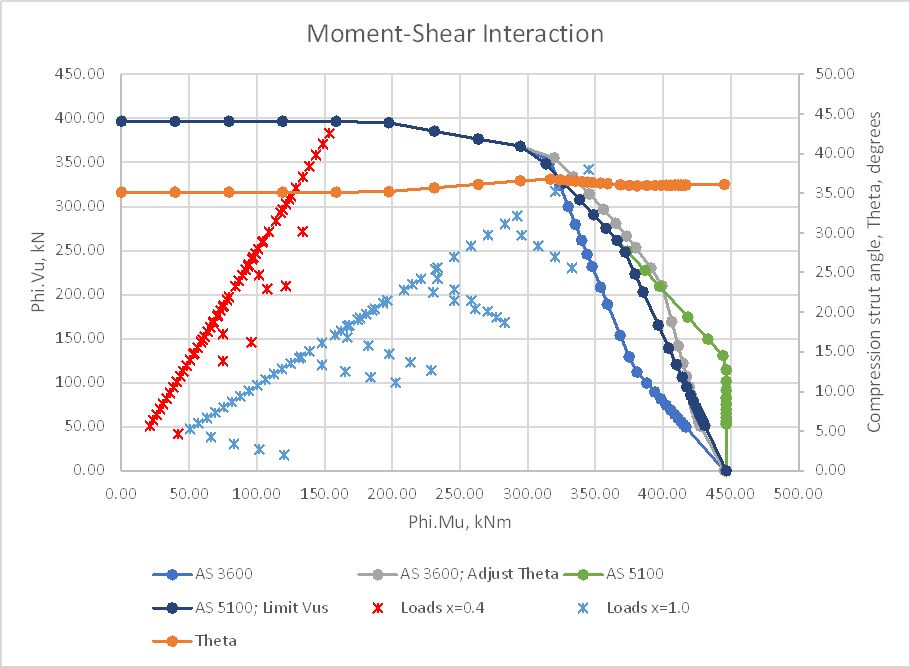
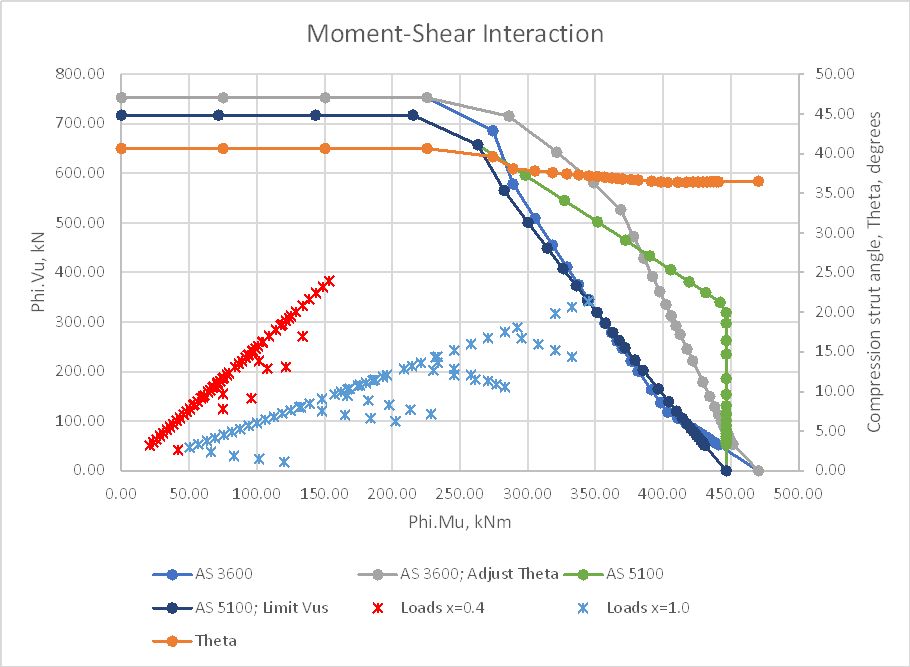
Increasing the shear steel diameter to 20 mm the trend of the results is similar except that in this case the AS 5100.5 results with a limit on Vus are significantly less than the AS 3600 results with adjustment of the strut angle. Note that if the strut angle was adjusted in the AS 5100.5 results (as allowed by the code) the results would be very close to the AS 3600 results. The AS 5100.5 results without a limit on Vus become unconservative for bending moments over 350 kNm in this case, with the applied shear force having no effect on the section capacity for a force of 350 kN or less:

Applying the code reduction factors for the AS 3600 calculations, with the same shear steel as above, the AS 3600 results without adjustment of the strut angle are very close to the AS 5100.5 results with the limit on Vus. AS 5100.5 results without the limit on Vus become lower than the AS 3600 results with adjustment of the strut angle, but again become unconservative for bending moments above about 380 kNm: