This post was prompted by an Eng-Tips question: Statically Indeterminant Beam Problem, asking for reactions due to a triangular distributed load on the middle span of a continuous beam with 3 equal simply supported spans. This could be simply solved with a frame analysis program, or continuous beam analysis (such as ConBeamU or py_ConBeamU), but it is useful to analyse this problem from first principles to get a better understanding of the procedures used.

The procedure used in my continuous beam spreadsheets is:

• Remove the internal supports so the beam can be analysed as a determinate simply supported single span.
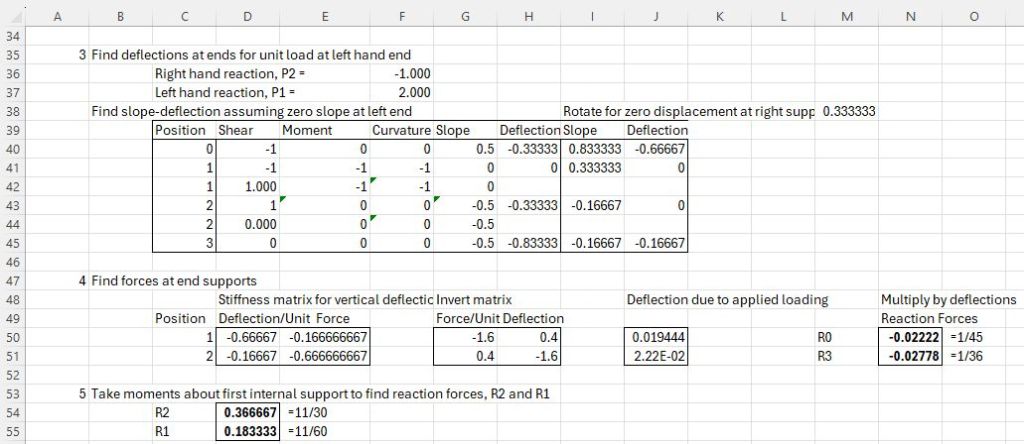
• Use the slope-deflection method to find the deflections at the internal support locations.
• Apply a unit load at each of the internal support locations in turn and find the deflection at all of the internal supports due to that load.
• Calculate the load required at each support to reverse the deflection due to the original applied load.
• Take moments about one end to find the reactions due to the applied loads and the internal support reactions.

Since the spans are equal in the given problem, the analysis can be simplified by

• setting the spans, the bending stiffness and the maximum load to a value of 1.
• Apply the triangular distributed load as a point load and moment at the two internal supports, based on the fixed end actions due to that load.

Note that:

• Slopes and deflections are found by initially assuming zero slope at the left-hand end, then rotating about the left-hand end for zero deflection at the other end.
• The calculated deflections due to unit load at the internal support are set up in a 2×2 stiffness matrix, which is inverted to find the force matrix for unit deflection, and this is then multiplied by the deflections due to the applied load, to find the reactions at the internal supports.

An alternative process is to remove the two end supports, and find the deflections at these locations due to the applied load on the middle span:

Finally a simple version of standard frame analysis procedure can be set up:

• Find the global stiffness matrix for bending about the horizontal axis at each support location.
• Invert this matrix and multiply by the moments at the internal supports due to the applied load, to find the slope at each support.
• Find the stiffness matrix for rotations and vertical deflections for one beam, and multiply by the rotations at each support to find the nett actions (shear force and bending moment) at each support.
• The reactions are then equal to: -nett action + applied load:

The calculated reactions are exactly the same from each of the three calculations. Copies of the spreadsheets used can be downloaded from: 3 Span triang load.zip