… with Excel, Python and pyxll.

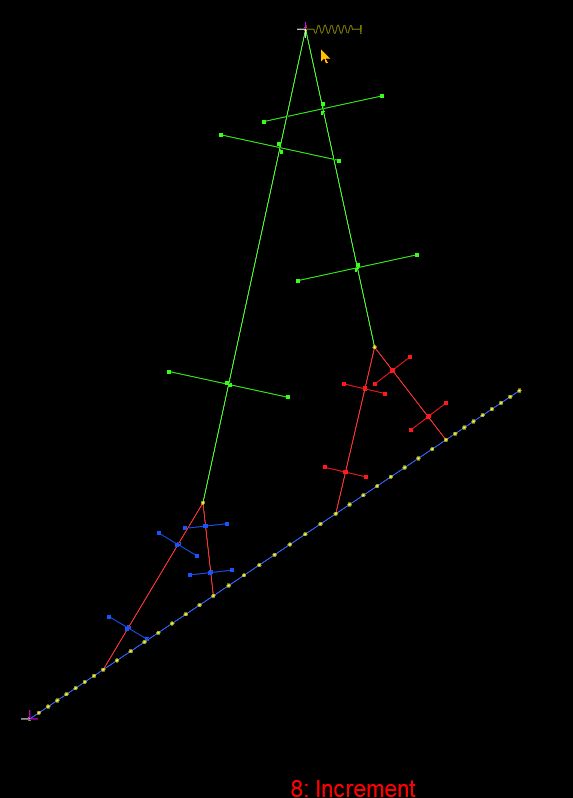
The problem involves the lifting of a precast concrete panel (or any other long thin object) with lifting points at four sections along the length of the panel, and with the load connected to the crane hook through 3 slings with 3 pulleys:

The spreadsheet 4PointLift.xlsb has been added to the py_SciPy download, along with two new Python functions added to the pyScipy3.py file. The updated files can be downloaded from:

py_SciPy.zip

The spreadsheet uses the pyxll add-in to call Python code from Excel. See pyxll for more details and download.

Assumptions in the analysis are:

• The pulleys have negligible friction.
• The crane lifting force at the top pulley is vertical.
• The panel rotates about the left end of the panel, which does not move horizontally.
• Bending deflections of the panel and axial deflections of the panel and slings are negligible.

With these assumptions it can be shown that:

• The legs of the top sling must have equal and opposite angles to vertical.
• Each leg of the top sling bisects the angle at the top of the attached lower slings.
• The total length of each sling is unchanged.

The required input data is:

• The length along the panel to each lifting point, measured from the left; L1 to L4 in the diagram above. L5 is only required for plotting the lift diagram.
• The three sling lengths.
• The angle of the panel to horizontal.
• Guessed coordinates for the 3 pulley positions, with origin at the left end of the panel.

With this data the XY coordinates of the 4 lifting points can be calculated:

The problem can be solved using the general purpose solver function py_SolveFS, together with the LiftCoords function. To use py_SolveFS the input must be rearranged to single column ranges, as shown above.

The function LiftCoords evaluates the six equations shown below.

py_SolveFS combines the Targets and Values arrays into a single list of lists which it passes to the Scipy root function, that passes the data onto LiftCoords, together with adjusted “Guess” data, until all the returned values are sufficiently close to zero.

def LiftCoords(x0, values):
    Target = values[0]
    knownvals = values[1]

    a, b, c, d, e, f, g, h = knownvals
    o, p, q = Target
    
    i, j, k, l, m, n = x0
    

    res = np.zeros(6)

    res[0] = ((((i-a)**2)+((j-b)**2))**0.5)+((((c-i)**2)+((j-d)**2))**0.5)-o
    res[1] = ((((k-e)**2)+((l-f)**2))**0.5)+((((g-k)**2)+((l-h)**2))**0.5)-p
    res[2] = ((((m-i)**2)+((n-j)**2))**0.5)+((((k-m)**2)+((n-l)**2))**0.5)-q
    res[3] = (m-i)/(n-j)-(k-m)/(n-l)
    res[4] = (2*(np.arctan2((n-j),(m-i)))-np.arctan2((j-b),(i-a))-np.arctan2((j-d),(i-c)))
    res[5] = (2*(np.arctan2((n-l),(m-k)))-np.arctan2((l-f),(k-e))-np.arctan2((l-h),(k-g)))

    return res

After root finds the solution to the 6 equations py_SolveFS returns the final 6 values (the XY coordinates of the 3 pulley locations) to the spreadsheet, together with estimated errors and solution time.

As an alternative to using py_SolveFS, I have written a problem specific function to allow the input and results to be in a more convenient format. Input and output for Solve4PointLift are shown above.

The results from the spreadsheet analysis shown above were checked using the Strand7 FEA program. After increasing the stiffness of the concrete and slings by a factor of 100, the Strand7 results were found to be within 0.25 mm of the spreadsheet solver results:

Strand7 plot: