The New Scientist brain twister from last weeks edition has several problems involving pandigital sums, which are additions that use each of the digits from 0 to 9 exactly once, and with no number within the sum that starts with a zero.
The problems can be solved without the use of computers, but it is also interesting to write code to generate brute force solutions, which is what is covered in this post. For anyone who wants to have a go at solving the problems themselves, the screenshot at the bottom of this post contains some solutions, so don’t scroll down.
The problems are:
- Find a pandigital sum of the form ABCD + EF = 2034
- There are 96 pandigital sums of the form ABC + DEF = GHIJ. How many of these have GHIJ = 1089
- Find the pandigital sum where ABC + DEF = GHIJ.and A<B<C<D<E<F.
My Python code and a sample spreadsheet with VBA code can be downloaded from:
I started off with the third problem, using VBA:
Function Pandigital()
Dim a, b, c, d, e, f, g, h, i, j, ResA(1 To 1, 1 To 5), STime
STime = Timer()
For a = 1 To 9
For b = a + 1 To 9
For c = b + 1 To 9
For d = c + 1 To 9
For e = d + 1 To 9
For f = e + 1 To 9
For g = 1 To 9
For h = 0 To 9
For i = 0 To 9
For j = 0 To 9
If (a + b + c + d + e + f + g + h + i + j = 45) Then
If (100 * a + 10 * b + c + 100 * d + 10 * e + f = 1000 * g + 100 * h + 10 * i + j) Then
ResA(1, 1) = 100 * a + 10 * b + c
ResA(1, 2) = 100 * d + 10 * e + f
ResA(1, 3) = ResA(1, 1) + ResA(1, 2)
ResA(1, 4) = 1000 * g + 100 * h + 10 * i + j
ResA(1, 5) = Timer() - STime
Pandigital = ResA
Exit Function
End If
End If
Next j
Next i
Next h
Next g
Next f
Next e
Next d
Next c
Next b
Next a
End Function
This works, and returns the answer in well under a second, but I wanted to avoid so many indented ifs, and also to optimise the code to reduce the number of trials where the values did not meet the stated criteria.
My first effort using Python (linked to Excel with pyxll) was:
@xl_func()
@xl_return('numpy_array')
def py_Pandigital0():
stime = time.perf_counter()
intlist = [0, 1,2,3,4,5,6,7,8,9]
abc = np.array([1,2,3])
def_ = np.array([4,5,6])
facta = np.array([100,10,1])
for k in range(0, 3):
if abc[0] < 4: abc[0] += 1
abc[1] = abc[0]
for l in range(0, 3):
if abc[1] < 5: abc[1] += 1
abc[2] =abc[1]
for m in range(0, 3):
if abc[2] < 6: abc[2] += 1
abcsum = np.dot(abc, facta)
for n in range(0, 3):
if def_[0] < 7: def_[0] += 1
def_[1] = def_[0]
for o in range(0, 3):
if def_[1] < 8: def_[1] += 1
def_[2] = def_[1]
for o in range(0, 3):
if def_[2] < 9: def_[2] += 1
defsum = np.dot(def_, facta)
sum1 = abcsum + defsum
sumlist = intlist.copy()
for p in range(0, 3):
if abc[p] in sumlist:
sumlist.remove(abc[p])
else:
break
if def_[p] in sumlist:
sumlist.remove(def_[p])
else:
break
for q in range(1, 4):
for r in range(0, 4):
for s in range(0, 4):
for t in range(0, 4):
sum2 = sumlist[q]*1000 + sumlist[r]*100 +sumlist[s]*10 + sumlist[t]
if sum1 == sum2:
etime = time.perf_counter() - stime
return np.array([abcsum, defsum, sum1, sum2, etime])
return np.array(sumlist)
The differences from the VBA code are:
- The values for the first two numbers are restricted to the possible ranges.
- The values are generated from the selected digits by multiplying two numpy arrays, using np.dot.
- The numbers available for the sum value are generated by removing the 6 digits of ABC and DEF from a list of digits from 0 to 9, using the list.remove method.
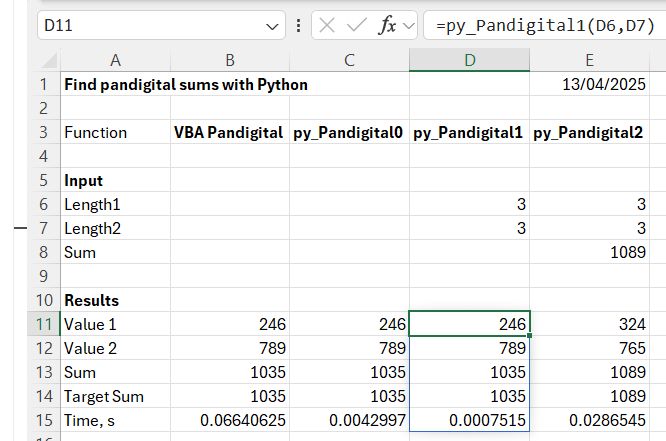
The Python code reduced the execution time from 66 milliseconds down to 4 milliseconds.
The Python code was further refined by using the itertools permutations and combinations methods to generate lists of trial groups of digits:
@xl_func()
@xl_arg('in_list', 'numpy_array', ndim=1)
@xl_arg('n', 'int')
@xl_return('numpy_array')
def Perms(in_list, n):
PermA = []
for perm in permutations(in_list,n):
PermA.append(list(perm))
return np.array(PermA)
@xl_func()
@xl_arg('in_list', 'numpy_array', ndim=1)
@xl_arg('n', 'int')
@xl_return('numpy_array')
def Combs(in_list, n):
CombA = []
for comb in combinations(in_list,n):
# if list(comb) == sorted(comb):
CombA.append(list(comb))
return np.array(CombA)
These two functions can also be called from Excel, and return all the combinations or permutations of the specified list from the given input list:
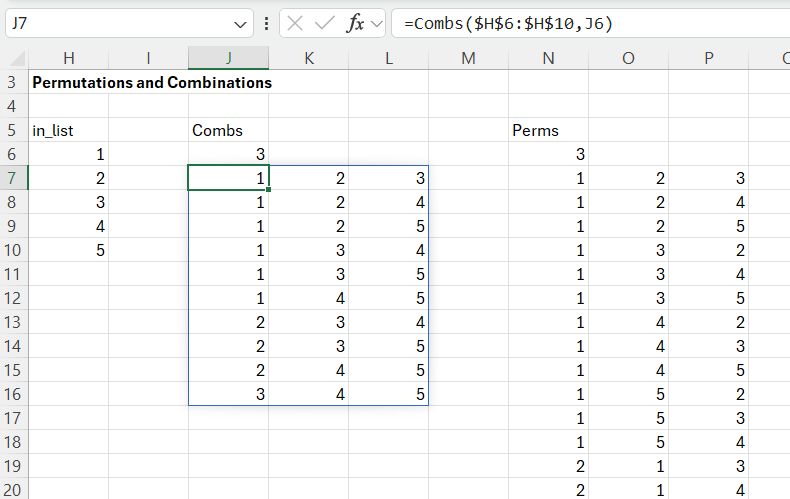
The Combs function returns all the groups of 3 numbers selected from the input list of 5 numbers, listed in the same sequence as in the input array;10 combinations are returned in this case. Note that the code has a commented out line, checking that the returned values are in increasing order. This was suggested by the Bing AI code generator, but was not necessary because the input list was in ascending order.
For more details on permutations and combinations see Combinations and Permutations
The Perms function returns the same 10 groups of numbers, but with each sorted in the 6 possible different orders, returning 60 permutations in all. In my code the Combs function is used to generate the first two numbers, but Perms is used for the final sum because this may be in any order, other than not starting with zero.
@xl_func()
@xl_arg('m', 'int')
@xl_arg('n', 'int')
@xl_return('numpy_array')
def py_Pandigital1(m, n):
stime = time.perf_counter()
intlist = np.array([0,1,2,3,4,5,6,7,8,9])
intlist1 = intlist[2:10-n]
intlist2 = intlist[m+2:]
abcA = Combs(intlist1, m)
defA = Combs(intlist2, n)
rows = abcA.shape[0]
rows2 = defA.shape[0]
o = 10 - (m+n)
facta1 = []
facta2 = []
facta3 = []
for i in range(m-1,-1,-1):
facta1.append(10**i)
facta1 = np.array(facta1)
for i in range(n-1,-1,-1):
facta2.append(10**i)
facta2 = np.array(facta2)
for i in range(o-1,-1,-1):
facta3.append(10**i)
facta3 = np.array(facta3)
for a in range(0, rows):
abc = abcA[a,:]
abcsum = np.dot(abc, facta1)
for b in range(0, rows2):
def_ = defA[b,:]
if def_[0] > abc[-1]:
defsum = np.dot(def_, facta2)
sum1 = abcsum + defsum
sumlist = intlist.copy().tolist()
for c in range(0, m):
if abc[c] in sumlist:
sumlist.remove(abc[c])
else:
break
for c in range(0, n):
if def_[c] in sumlist:
sumlist.remove(def_[c])
else:
break
SumA = Perms(sumlist, 4)
rows3 = SumA.shape[0]
for d in range(0, rows3):
SumA2 = SumA[d, :]
if SumA2[0] == 1: # > 0:
sum2 = np.dot(SumA2, facta3)
if sum1 == sum2:
etime = time.perf_counter() - stime
return np.array([abcsum, defsum, sum1, sum2, etime])
etime = time.perf_counter() - stime
return np.array(etime)
In addition to the use of the combinations and permutations method, this code has also been modified to allow the length of the output numbers to be changed, for instance to check if there was a solution of the form ABCD + EF (there wasn’t). The execution time for this code comes down to 0.8 milliseconds.
For the first two problems the generated values do not need to be in increasing order, but the resulting sum is specified in the input:
@xl_func()
@xl_arg('m', 'int')
@xl_arg('n', 'int')
@xl_arg('sum2', 'int')
@xl_return('numpy_array')
def py_Pandigital2(m, n, sum2):
stime = time.perf_counter()
intlist = [0,1,2,3,4,5,6,7,8,9]
sum2A = np.array([int(d) for d in str(sum2)])
s = sum2A.shape[0]
for i in range(0, s):
intlist.remove(sum2A[i])
abcA = Perms(intlist, m)
defA = Perms(intlist, n)
rows = abcA.shape[0]
rows2 = defA.shape[0]
facta1 = []
facta2 = []
facta3 = []
for i in range(m-1,-1,-1):
facta1.append(10**i)
facta1 = np.array(facta1)
for i in range(n-1,-1,-1):
facta2.append(10**i)
facta2 = np.array(facta2)
for i in range(s-1,-1,-1):
facta3.append(10**i)
facta3 = np.array(facta3)
for a in range(0, rows):
abc = abcA[a,:]
for b in range(0, rows2):
def_ = defA[b,:]
if np.intersect1d(abc, def_).size == 0:
if np.intersect1d(abc, sum2A).size + np.intersect1d(def_, sum2A).size == 0:
abcsum = np.dot(abc, facta1)
defsum = np.dot(def_, facta2)
sum1 = abcsum + defsum
if sum1 == sum2:
etime = time.perf_counter() - stime
return np.array([abcsum, defsum, sum1, sum2, etime])
etime = time.perf_counter() - stime
return np.array(etime)
Changes in this code are:
- The trial values are generated with the permutations method, because their digits do not need to be in increasing order.
- The sum value is input, but this has to be checked against the two generated values to check that no digits are repeated. This is done with the numpy intersect1d function, which counts how many values two arrays have in common.
- The input sum value was split into an array of digits, which were then removed from the list of digits available for the first two numbers.
The reduced time for creating and checking the sum value was more than offset by the options for the first two numbers coming from a permutations list rather than combinations, and the execution time increased to 28 milliseconds.
Output results (spoiler alert: includes answers to the problems)