Following the previous post, the py_RC Design spreadsheet has been updated with improved versions of the py_UMomp and py_UMomBiax functions. The revised version can be downloaded from:

py_RC Design.zip

The py_UMomp function is based on the Umom function, with the following changes:

• The Eurocode 2 parabolic stress block is applied over the full range of axial loads and includes the required restrictions on maximum strain for neutral axis positions outside the concrete section. It may also be applied for calculations otherwise following the AS 3600 or AS 5100.5 codes.
• The reinforcement may now be distributed over any number of layers.
• The current version allows only for rectangular sections, but future versions will also have the option to specify any number of trapezoidal concrete layers.

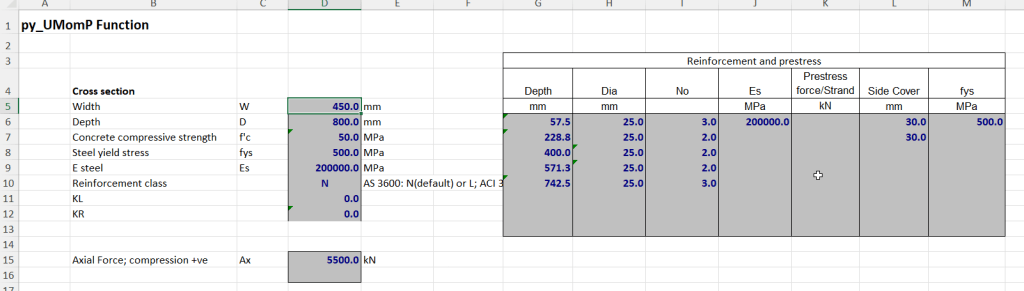
py_UMomp input:

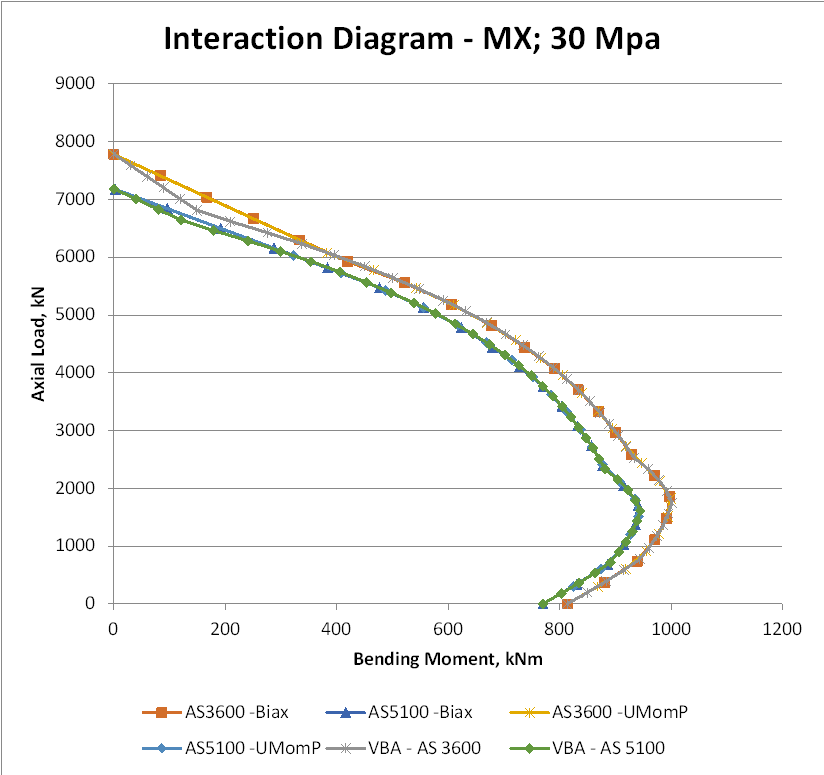
The results from the new function have been compared with the py_UmomBiax function (with the neutral axis angle set to zero) and also the VBA version of the UMom function.

With rectangular stress blocks used for all versions there is excellent agreement over most of the range, other than for high axial loads where the VBA version uses a different procedure for linear interpolation when the NA position is outside the concrete section:

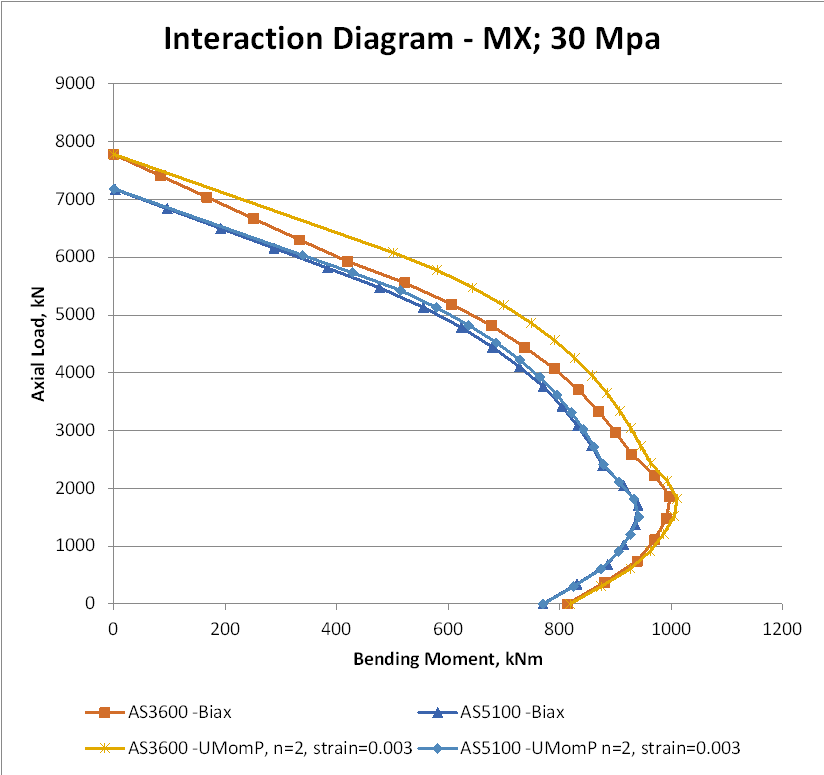
Comparing results using the parabolic-linear stress block with the rectangular stress block, but applying Australian code stress limits in both cases, there are significant differences for axial loads above the balance load, especially for AS 3600:

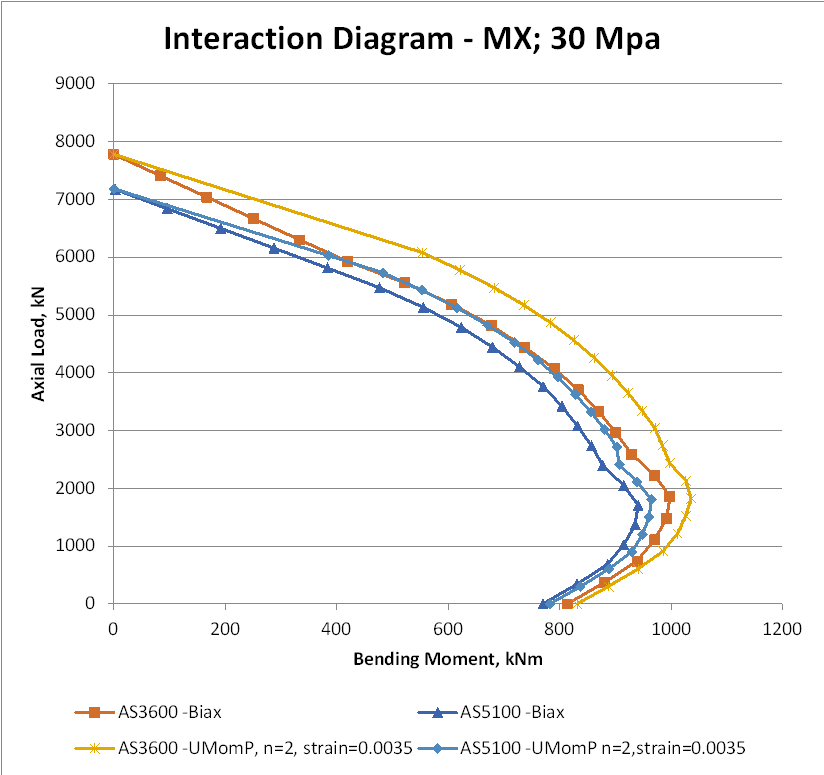
The differences are increased when the maximum strain is increased to the Eurocode 2 limit of 0.0035:

The difference between the AS 3600 and AS 5100.5 results is largely due to the difference in the default reduction factors. In the graph below the results for both codes have the AS 3600 values: 0.85 for zero axial load, reducing to 0.65 for sections where the concrete compression controls the design capacity.

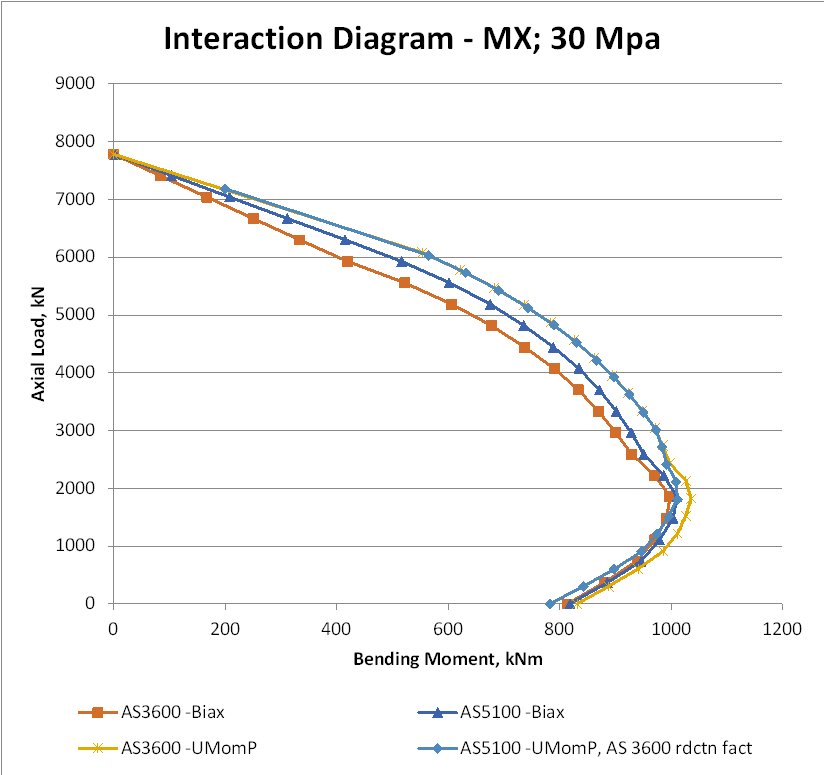
With 30 MPa concrete, results up to the balance load are now very close, with the AS 3600 results with a parabolic-linear stress block being higher than AS 5100.5 because of differences in the application of the transition of the reduction factors from 0.85 to 0.65. Above the balance load the two codes give identical results with the parabolic-linear stress block, but AS 3600 is significantly more conservative with the rectangular stress block.

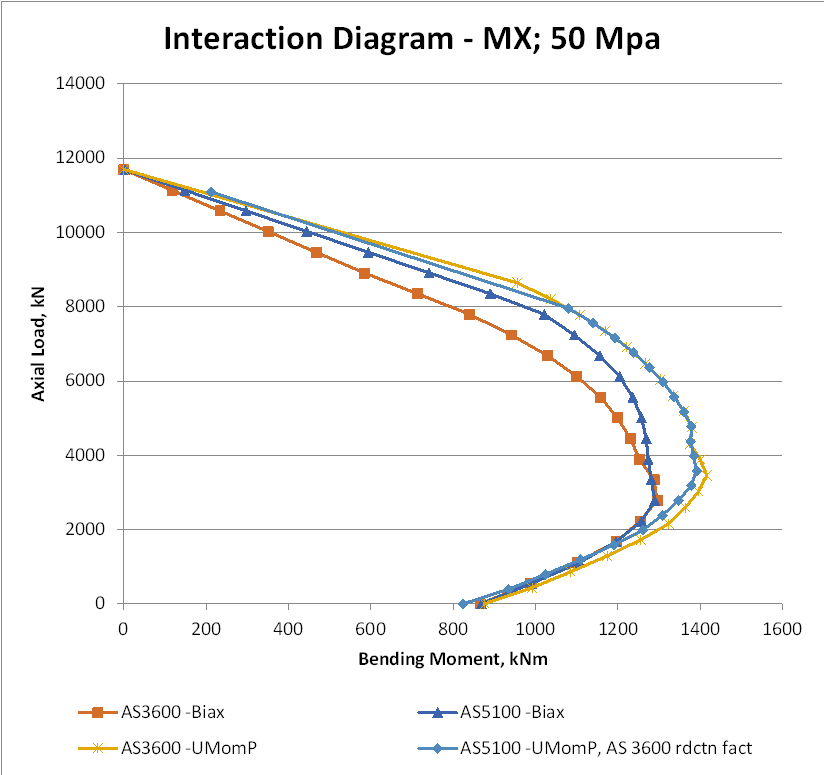
With 50 MPa concrete the differences are similar but the differences between two stress blocks are increased, and the difference between AS 3600 and AS 5100.5 with the rectangular stress block is also increased.

Finally with 90 MPa concrete all four results are very close over the full range.