RC Design Functions 9.03; compression strut angle adjustment

Posted on 11/11/2022 by dougaj4

The RC Design Functions spreadsheet has now been updated to Version 9.03, and is available for free download from:

RC Design Functions9.zip

The new version includes a number of corrections to the calculation of beam shear and torsion capacity to AS 3600 and AS 5100.5:

  • Shear capacity under negative bending moments has been corrected.
  • The sign of reported shear capacity is now the same as the input shear force (previously any input with negative moment returned a negative shear capacity).
  • The contribution of any negative torsion to longitudinal tension forces, to AS 3600, was taken as zero. This is actually in accordance with equation 8.2.7(3) of the code (since Amendment 2), but clearly the absolute value of the torsion should be used.

In addition, the new version allows the minimum angle of the concrete compression strut to be specified, between 29 and 50 degrees. The specified angle is used to calculate a minimum value for the mid-depth strain, which is also used in the calculation of the kv factor. Increase in the mid-depth strain value is allowed under Cl. 8.2.4.2 in both AS 3600 and AS 5100.5.

Use of the compression strut angle adjustment is shown in the screen-shots below:

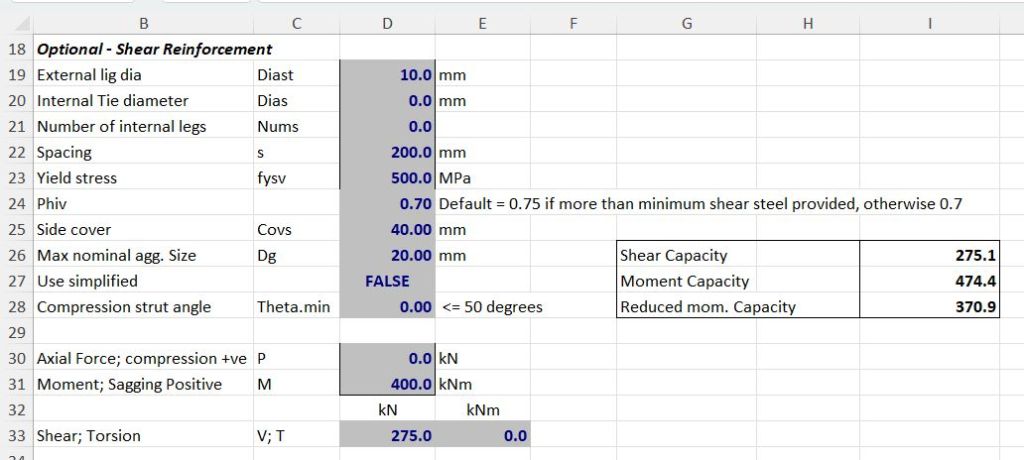
A beam has design loads of 400 kNm bending moment, and 275 kN shear force. With 10 mm shear reinforcement the shear capacity is just adequate, but taking account of the longitudinal forces due to shear the bending capacity is reduced to 371 kNm:

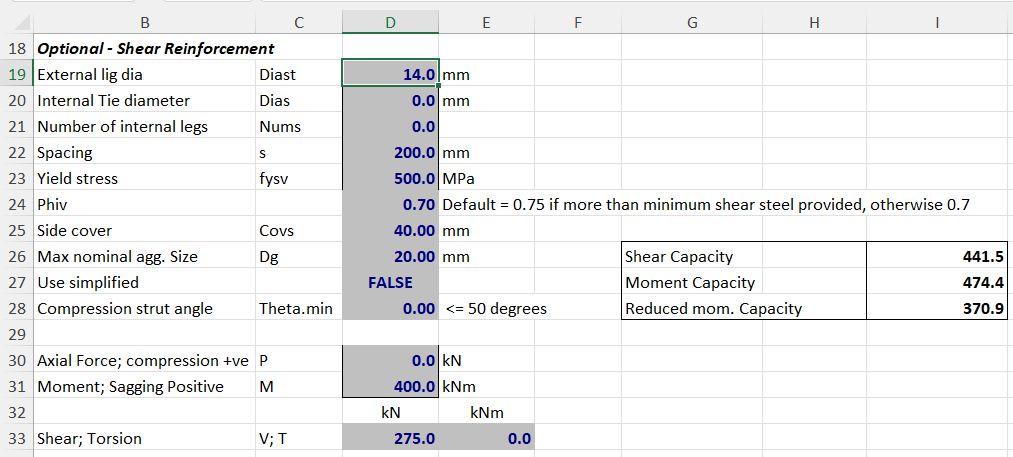
Increasing the shear reinforcement to 14 mm diameter increases the shear capacity, but using the code calculated compression strut angle to AS 3600 the reduced bending capacity is unchanged. (Note that AS 5100.5, and earlier versions of AS 3600, have a substantial increase in the bending capacity when the shear reinforcement is increased. This is discussed further below):

Entering a compression strut angle of 49.6 degrees (with the “Use simplified” option set to “False”) reduces the shear capacity back down to the required value (275 kN), but the moment capacity is now increased to 416 kNm. Note that any further increase in the shear reinforcement would have negligible effect (to AS 3600) because the compression strut angle is already very close to the maximum value of 50 degrees:

The effect of increasing the shear reinforcement on the adjusted bending capacity with different codes and approaches is shown in the graph below:

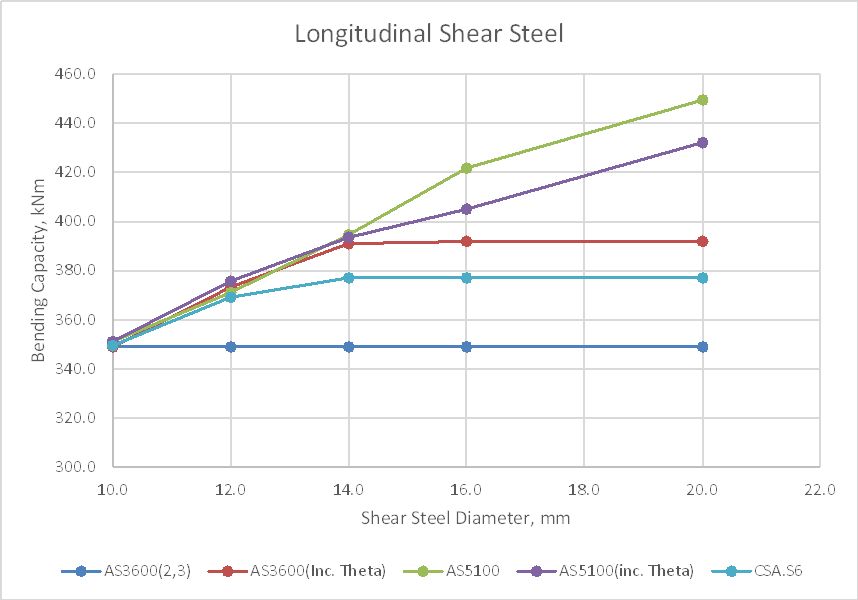
The lines are:

  • 1) AS 3600, Amendment 2 or 3, default compression strut angle.
  • 2) AS 3600 with compression strut adjusted to maintain constant shear capacity.
  • 3) AS 5100.5, default compression strut angle.
  • 4) AS 5100.5 with adjusted compression strut angle.
  • 5) As 3), but shear reinforcement force limited in accordance with the Canadian Bridge Code.

So what is going on here?

In AS 5100.5 (and AS 3600 up to Amendment 1) the longitudinal force due to shear is defined as:

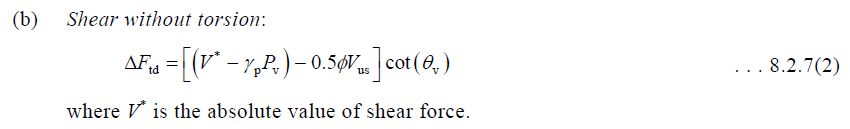
Vus is proportional to the area of shear steel, and is not limited, so increasing the shear steel area allows the value of DeltaFtd to be reduced to zero, even though in reality the actual force in the steel cannot be greater than the applied shear force (V*) minus the concrete shear force. The large increase in bending capacity with increased shear steel shown by line 3) is therefore not realistic.

Increasing the compression strut angle (Thetav) with the AS5100.5 equation reduces cot(Thetav), which reduces Vus, but also reduces DeltaFtd. The resulting calculated bending capacity is still unrealistic for large areas of shear reinforcement.

In AS 3600 Amendment 2 the equation for longitudinal force due to shear was revised to:

If the shear capacity of the section is exactly equal to V* then this equation is equivalent to the AS5100.5 version, but increasing the area of the shear reinforcement has no effect on Vuc, so there is no reduction in DeltaFtd, and the bending capacity remains constant, as seen in line 1.

In this case however increasing Thetav, which reduces cot(Thetav) reduces both Vuc and the resulting value of DeltaFtd. Increasing the shear reinforcement area therefore allows Thetav to be increased (so that the shear capacity remains equal to the design shear force), which reduces DeltaFtd, with the nett result that the bending capacity is very close to the values found from the AS 5100.5 equation, until Thetav reaches the upper limit of 50 degrees, after which the bending capacity remains constant (line 2).

Finally the Canadian Code requires the value of Phi.Vus to be limited to V*. In this case this restriction is more conservative than the approach taken in AS 3600. Bending capacities are similar to the other results for small shear reinforcement areas, but the maximum bending capacity is significantly lower than that found with AS 3600 with adjustment of the compression block angle.

In summary:

  • The AS 3600 equation with default compression block angle is conservative, but shows no benefit from increased shear reinforcement area.
  • Applying adjustments to the compression block angle, in accordance with the code, the AS 3600 equation gives results very close to those from AS 5100.5, up to a reasonable limit (i.e. maximum angle of 50 degrees, equivalent to a maximum mid-depth strain of 0.003).
  • If the shear reinforcement area is increased well above the area required for the design shear force the AS 5100.5 equation gives bending capacity results that are highly unconservative.
  • If design is required to follow the current AS 5100.5 (Amendment 1), it is recommended that the Canadian code limit (Phi.Vus < V*) be applied.
Posted in Beam Bending, Concrete, Excel, Newton, UDFs, VBA | Tagged , , , , , , , , | 2 Comments

Linking to Python help from Excel

Posted on 06/11/2022 by dougaj4

The py_Numpy spreadsheet presented in the previous post has been updated:

  • A large number of Numpy functions added.
  • Return function help documentation to the spreadsheet for a selected function.
  • View Numpy on-line documentation from the function Wizard.

The new version can be downloaded from:

py_Numpy.zip

As before, the pyxll add-in is required for the connection from Excel to Python.

All the available functions are listed on the first sheet. Enter the index number for a function in cell F4, and the help for that function will be displayed:

The on-line help for all the listed Numpy functions can also be accessed quickly and easily through the Function Wizard.

Select a function and click on the “Insert Function” icon (immediately to the left of the Edit bar):

Then click “Help on this function” in the bottom left corner:

The Numpy on-line help for the selected function is displayed.

Note that this is a work in progress. Connecting to the on-line help requires a different html path to be generated for each function, and the path names are not always consistent. If you find any Numpy functions where the help is not displayed, please let me know.

Posted in Excel, Link to Python, Newton, NumPy and SciPy, PyXLL, UDFs | Tagged , , , , , , | Leave a comment

Calling Numpy polynomial functions from Excel

Posted on 31/10/2022 by dougaj4

The Numpy polynomial related function discussed in recent posts can now be downloaded from:

py_Numpy.zip

The download file includes Python code and a sample spreadsheet. Required installed software is Python, Numba and pyxll to call the code from Excel. Some of the functions in the default file require the just-in-time compiler, Numba. For those without Numba installed the file pyNumpy-noJIT.py can be used.

Note that the Quadratic, Cubic and Quartic functions (which are not included in Numpy) are based on C code from the following sources:

The screenshots below show examples of the spreadsheet functions: (click on any image for full-size view).

The py_PolyRoots function calls the general purpose Numpy function, that will work for any degree polynomial. The alternative functions have very much better performance for degrees up to quartic.

Py_PolyFromRoots finds polynomial factors from its roots. Py_PolyVal returns the function value for any value of x, allowing array input.

Py_PolyFit fits a polynomial to input data:

Other Numpy polynomial functions are shown below:

The py_flip functions reverses a Numpy array along a specified axis:

Finally functions are provided to form a Numpy array of complex numbers from an Excel list of pairs of floats:

Posted in Curve fitting, Excel, Link to Python, Maths, NumPy and SciPy, PyXLL, UDFs | Tagged , , , , | 1 Comment

Solving cubic equations – background and timing

Posted on 25/10/2022 by dougaj4

For more information on the polynomial functions, including quartic and higher order solvers, see: Solving Quadratic, Cubic, Quartic and higher order equations; examples

Re-reading the Wikipedia article on solving cubic equations, I noticed that the trigonometrical solution for finding 3 real roots seemed a very simple approach, which might be faster than the current code in my current VBA cubic function. (See Cubic Equations). Writing a new CubicT function, I found that this was actually slower than the original function (see more details below), and checking the code I found the original method for finding 3 roots was essentially the same as the Wikipedia method, and the method for 1 real root was simpler. Nonetheless, the code for the new function was better documented than the older code, so I have added the new function and a sheet documenting the method to the download file at:

Polynomial.zip

Times for 100,000 iterations of the new function are shown below, compared with the Cubic function (which returns the same results), CubicC (which also returns complex roots), and the Quartic function:

The VBA version of the CubicT function is more than twice as slow as the original Cubic function, presumably because the routine for finding single real roots is slower.

The code for all four functions was transferred to Python (called from Excel with pyxll), and as is typical with plain (and non-optimised) Python code, the performance was 2-3 times slower.

Modifying the Python code to use the Numba JIT compiler gave a substantial performance improvement, with the Python code now 2-5 times faster than the VBA. The CubicT function with Numba was greatly improved, and was slightly faster than Cubic. The Quartic function had an even greater improvement, and was faster than the CubicC function, and only a little slower than the other two Cubic functions.

Two Python functions also called the Numpy general purpose polynomial routines. These were both very slow, presumably because the solvers are written for polynomials of any degree, and are not optimised for cubic or quartic equations.

Note that the download file includes all the new VBA code, but not the new Python functions. This will be covered in a future post.

Posted in Excel, Link to Python, Maths, Newton, NumPy and SciPy, PyXLL, UDFs, VBA | Tagged , , , , , , , , , | Leave a comment

Working with Python polynomials from Excel

Posted on 22/10/2022 by dougaj4

Python polynomial functions have several features that require manipulation of data passed from Excel:

  • In Python polynomial coefficients are listed in order of increasing powers of x (a + bx + cx^2 …), but they are more usually listed with the highest power first, including in my VBA polynomial functions.
  • Polynomial functions may have complex numbers as input, and often have complex output, but Excel complex numbers are limited in functionality and are displayed as text strings, which makes use of the values on the spreadsheet difficult. A more convenient format is to pass complex numbers to and from Python as pairs of floats, or 2D arrays of floats.

I have written 3 short Python functions to deal with passing arrays of complex numbers from and to Excel, using pyxll, or within Python code to convert arrays of pairs of floats to Python complex format.

The py_ReverseA function reverses a 1D or 2D array, and with a 2D array the axis to be reversed may be specified, or by default the longer axis is used:

@xl_func
@xl_arg('array1', 'numpy_array')
@xl_arg('axis', 'int')
@xl_return('numpy_array')
def py_ReverseA(array1, axis = None):
    ndims = len(array1.shape)
    if ndims == 1:
        return array1[::-1]
    else:
        if axis == None:
            axis = 0
            if array1.shape[1] > array1.shape[0]: axis = 1
        if axis == 0:
            return array1[::-1,:]
        else:
            return array1[:, ::-1]

py_FloatA2Complex converts an Excel range of values to a Python complex array. If the Excel range is a single column the values will be converted to complex numbers with an imaginary value of zero. Ranges with 2 columns or 2 rows will have pairs of values converted to Python complex values:

@xl_func
@xl_arg('array1', 'numpy_array', ndim = 2)
@xl_arg('axis', 'int')
@xl_return('var')
def py_FloatA2Complex(array1, axis = None):
    rows, cols = array1.shape
    if axis == None:
        if rows > 2 or rows >= cols:
            axis = 0
        else:
            axis = 1
    if axis == 0:
        complexa = np.zeros(rows, dtype=np.complex128)
        if cols > 1:
            complexa[:] = array1[:, 0] +1j*array1[:, 1]
        else:
            complexa[:] = array1[:, 0] +1j*np.zeros(rows)
    else:
        complexa = np.zeros(cols, dtype=np.complex128)
        if rows > 1:
            complexa[:] = array1[0, :] +1j*array1[1, :]
        else:
            complexa[:] = array1[0, :] +1j*np.zeros(cols)
    return complexa

Note that this function returns an array of complex numbers, which are primarily intended for use by other Python functions. If it is called from Excel it will return a cache object, displaying as “ndarray@18”. This can be returned back to Python, or another Python function (such as py_Complex2FloatA below) can be used to extract the data in a format that can be displayed by Excel.

Finally, py_Complex2FloatA converts a Python array of complex numbers to a 2 column or 2 row range of Excel doubles:

@xl_func
@xl_arg('array1', 'var')
@xl_arg('axis', 'int')
@xl_return('var')
def py_Complex2FloatA(array1, axis = 0):
    rtn = np.array([array1.real, array1.imag])
    if axis == 0: rtn = np.transpose(rtn)
    return rtn

The screenshot below shows examples of each of these functions:

Posted in Arrays, Excel, Link to Python, PyXLL, UDFs | Tagged , , , , , , , , , | Leave a comment