I have now transferred the Ultimate Limit State design functions from the VBA RC Design Functions spreadsheet to Python format. The new spreadsheet and Python code can be downloaded from:
The code also includes the OptShearCap3600 function, described in the previous post.
The python code requires pyxll to connect to Excel. If this is installed, and “RC_UMom” is added to the list of modules to load at start-up in the pyxll.cfg file, the new functions should be available from any spreadsheet.
The included functions are:
py_UMom: ULS design of rectangular sections with two layers of reinforcement under combined bending, axial load, shear and torsion, to Australian and international codes. (Provision for prestressing will be added in the near future):
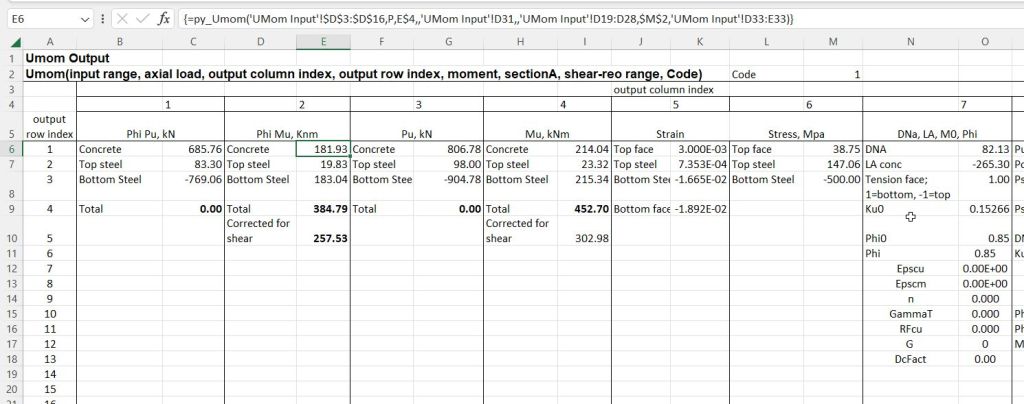
py_UmomPF: As above, but for Eurocode and British codes using a partial factor approach:
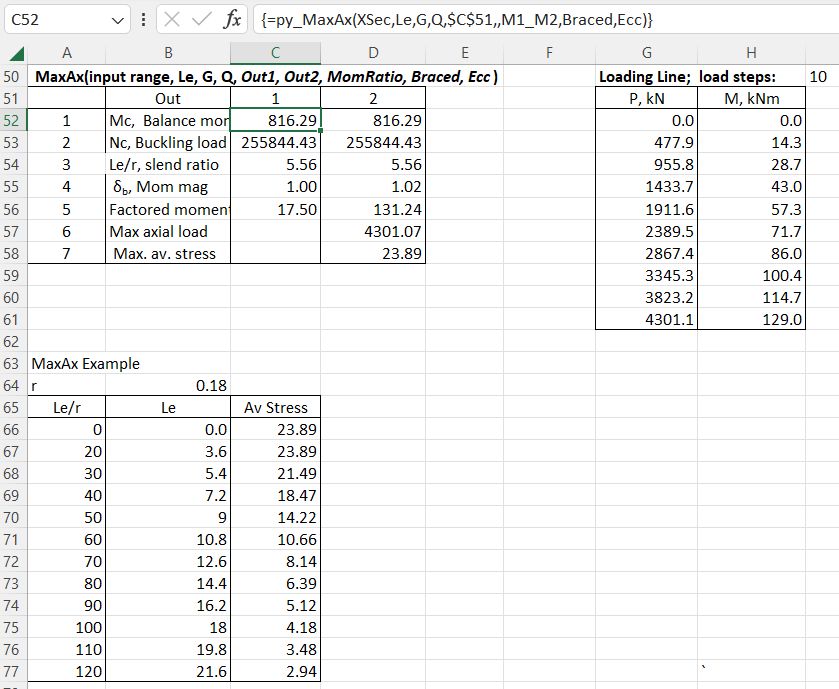
MaxAx: Maximum axial load for short or slender columns:
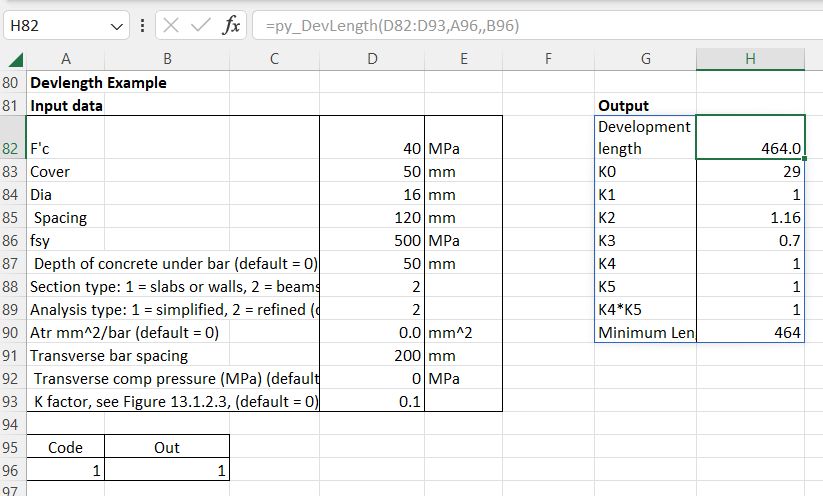
Devlength: Reinforcement development length to Australian, Eurocode, or British codes:
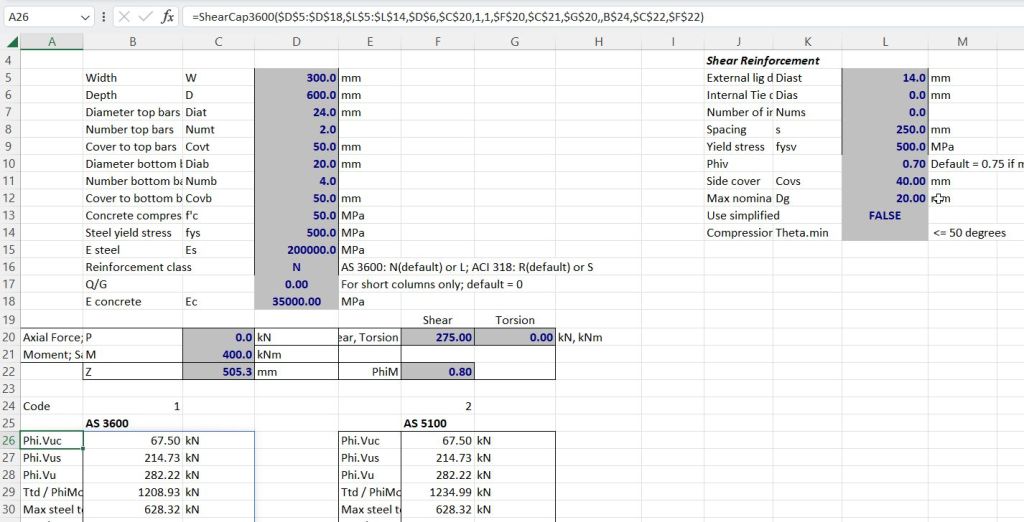
ShearCap3600: Shear capacity to current AS 3600 and 5100.5:
OptShearCap3600: Optimise shear capacity for given moment/shear ratio by adjusting the compression strut angle:
Extracts of the OptShearCap3600 function code are shown below. The scipy.optimize.brentq function is used to adjust the applied loads to be equal to the design section capacity:
# create list of arguments for the py_Umom function, called by the Scipy brentq function
args = [InCells, Puin, 13, 1, Muin, [] , ShearReo, Code, VTuin]
# Use scipy.optimize.brentq to adjust the input shear force to be equal to the design capacity
try:
res = sopt.brentq(call_Umom, mincap, maxcap, args = args, maxiter = 100)
except:
outA[0,0] = 1
return outA
# The call_Umom function adjusts the input loads in proportion to the shear force
# passed by brentq, then calls py_Umom and returns the difference between the
# applied shear and shear capacity
def call_Umom(Vstar, args):
args[8][0,0] = Vstar
args[4][0] = Vstar * MoV
if ToV != 0: args[8][0,1] = Vstar * ToV
if PoV != 0: args[1][0] = Vstar * PoV
res = py_Umom(*args )
return res[1]
Similar procedures are used to adjust the applied moment when this is critical, or the compression strut angle in the intermediate range, so that both shear and moment capacities are equal to the applied actions.
Further to the last post on this subject I have been looking at procedures to speed up design for shear to AS 3600 when the “refined” analysis procedure is used. The issues that need to be addressed are:
The design shear capacity reduces with increasing tensile strain at the mid-depth of the section, and the tensile strain increases with increasing applied moment and shear force. To find an accurate upper limit to the shear capacity it is therefore necessary to carry out an iterative analysis to match the applied shear force, and associated bending moment, with the shear capacity of the section. This is particularly important for the assessment of existing structures, where it is a requirement to find the actual maximum capacity of the structure, rather than designing for predefined maximum loads.
The maximum shear capacity may be controlled by the shear failure or by the combined effect of bending, shear and torsion on the longitudinal force on the tensile reinforcement.
As discussed previously, where the section capacity is controlled by the longitudinal tension force the design capacity can be increased by increasing the angle of the shear compression strut. This also requires an iterative process.
I have now written a Python function to carry out the iterations using the Scipy brentq function with the procedure outlined below:
From the input data calculate the ratios: moment/shear (M/V) and torsion/shear (T/V)
Adjust the shear force and associated actions so that the applied shear force equals the design shear capacity.
If the design bending capacity, reduced for the longitudinal force due to shear and torsion, is greater than the applied moment then return the results, else:
Set the shear compression strut angle to the maximum value allowed by the code (50 degrees) and adjust the shear force and associated actions so that the applied moment is equal to the reduced design bending capacity.
If the design shear capacity is now greater than the applied shear force then return the results, else:
Adjust the shear compression strut angle so the ratios Applied Shear/Design Shear Capacity and Applied Moment/Design Moment Capacity are equal.
Adjust the shear force and associated actions so that the applied shear force equals the design shear capacity.
Repeat 6 and 7 until the ratio of applied actions/design capacity equals 1 for both shear and bending.
Typical function output is shown in the screenshot below:
In this example the section has been analysed for a constant shear force with an increasing M/V ratio. The function output (Columns K to O) is:
Design shear capacity, and the associated bending moment for the input M/V ratio.
The “excess capacity” for shear and bending. Note that this has three zones where the capacity is initially controlled by shear only, then both shear and moment are at full capacity, then the adjusted bending capacity controls.
The compression strut angle (Theta). The strain values in Column P are calculated with a simple on-sheet formula.
These results are plotted below with typical shear and bending loads, taken from a heavy road vehicle travelling over an 8 metre simply supported span, with the loads plotted at 0.4 and 1.0 metres from the support. The capacity is also plotted with no adjustment of the compression strut angle, showing a significantly reduced capacity.
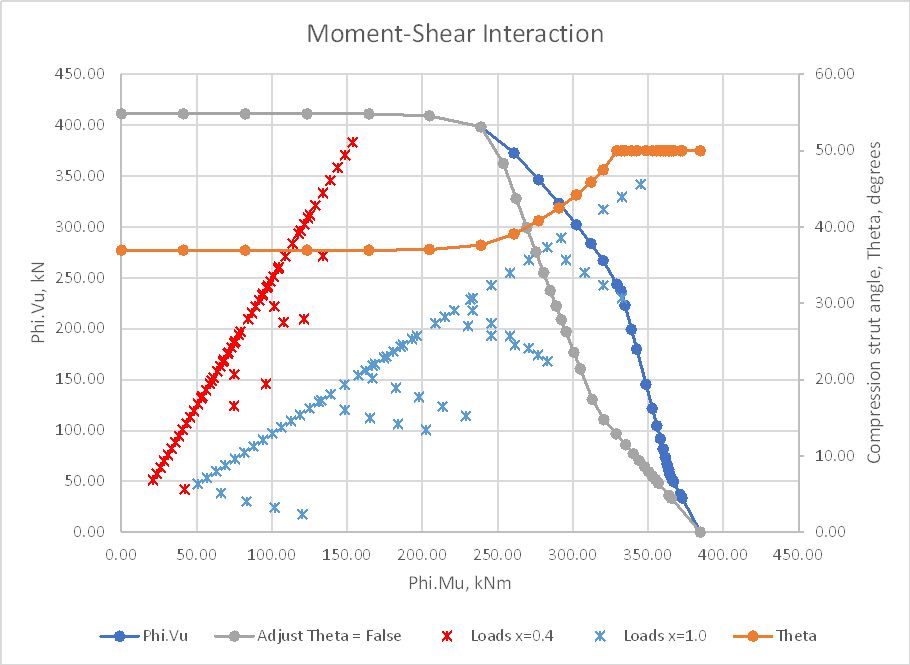
Plotting the section capacity as a moment-shear interaction diagram allows the loads from all sections with identical reinforcement to be plotted on the same section, and load cases where the applied loads exceed the section capacity are immediately visible.
This is a work in progress, but a spreadsheet with all necessary Python files will be available for download shortly.
There have been many posts here looking at alternative ways of working with functions entered as text on a spreadsheet, and working with units, most recently here.
One drawback with this approach is that text in an Excel cell must be ASCII or Unicode, which has limited capabilities for presenting maths text in a readable form. Excel does allow elaborate maths equations to be generated and displayed, but as far as I know there is no way to interact with these equations from VBA, so they can neither be generated by code, or evaluated by code.
Python on the other hand has libraries that will convert plain text equations to Latex (and other formats), and display Latex code. I have now written a Python function “plot_math” using a combination of Sympy, Pint, and Matplotlib to:
Read any maths function from the spreadsheet
Convert the text to Latex format
Return a graphic image of the function
Optionally evaluate the function using a table of values for each parameter
Optionally adjust for the units of the input and output values.
Startup_min.py includes the plot_math function, and should be added to the list of files to open at start-up in pyxll.cfg.
Note that this is a work in progress. If you have any problems with installation or running the programs, please let me know.
Some examples of the new function in action are shown below:
The text to be displayed (and optionally evaluated) should be entered as plain text at any chosen location. In the example below the plot_math function is then entered in the cell immediately above (C12).
When the plot_math function is entered the image will display immediately below:
The image can then be dragged to the desired location; in this case so that the original text and the function return value (0) are hidden. In this example the numerical value of the function for selected input values is displayed using the py_Evalu function.
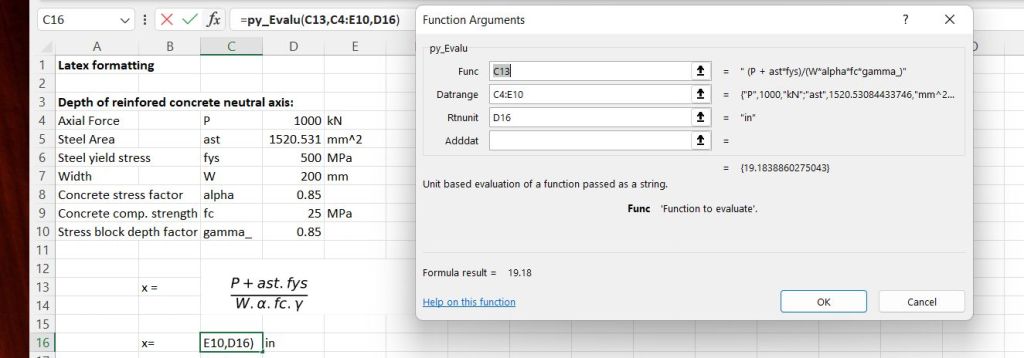
Alternatively the plot_math function will return the value of the function if suitable input data is selected:
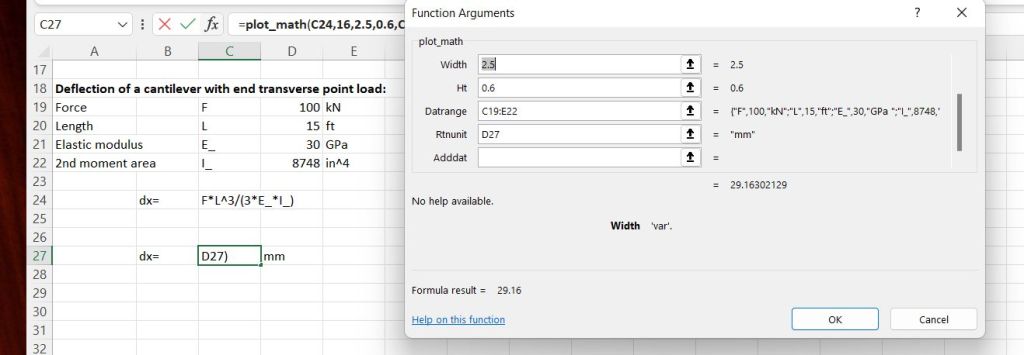
In this case a three column data range has been selected, and also an output unit, so the calculation will be unit aware:
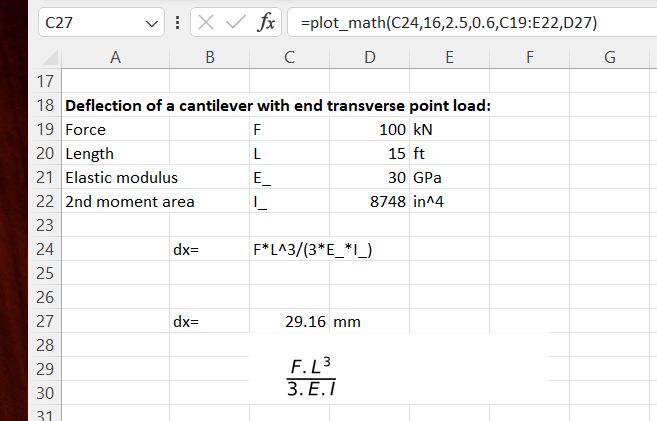
As before, the image is displayed immediately below the plot_math input cell, but can be dragged to any desired location:
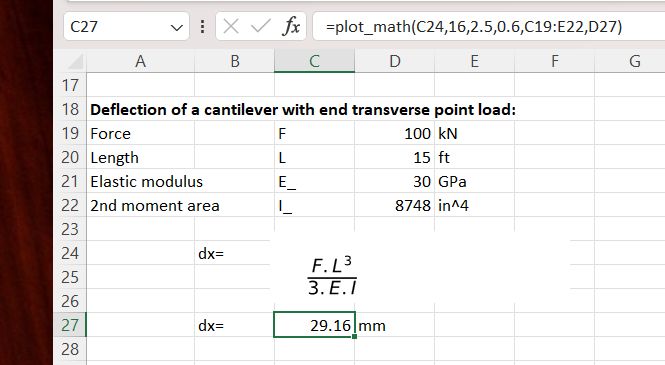
Some other features to note:
If the data range has only two columns (variable name and value) the calculation will have no units.
If the output unit is omitted, and the data range has three columns including units, the output value will be in base SI units.
Names of Greek letters (e.g. alpha) will generate the Greek character
In some case Greek letter names will be the name of a standard maths function (e.g. Gamma), in which case the text should be followed by an underscore (gamma_)
Some English letters also represent standard maths values (e.g. e and i). If an upper-case E or I is required, these should be entered followed by an underscore, and will then be displayed in upper-case, without the underscore.
The exponentiation symbol may be entered in either Excel (^) or Python (**) format. In either case the exponent will display as a superscript, and the calculation will be correct
Newton Excel Bach, not (just) an Excel Blog 