The principal axes of a beam (or any 2D closed shape) are defined as the axes along which an applied load will not cause any deflection in the transverse direction.  In mathematical terms, if the beam cross-section is defined in the XY plane, then the product of area Ixy is zero when the principal axes are coincident with the X and Y axes.  See Fundamentals of Beam Bending for more details.

In a 2D frame analysis it is assumed that one of the principal axes of  each beam is in the plane of the analysis, so that in-plane loads do not cause any out of plane deflection.  In a 3D analysis deflections in all 3 directions are taken into account, so it is necessary to define the orientation of the principal axes to the global axes used to define the beam positions.  One way to do this unambiguously is to define each beam with three nodes, where nodes 1 and 2 define the longitudinal axis and direction of the beam, and the plane defined by all three nodes defines the plane of Principal Axis 1.   This procedure requires significant additional data input, and since in most cases the planes of the principal axes will be vertical and horizontal, it is possible to define default directions for the principal axes, and then provide an angle of rotation for any beams where the principal axes do not lie in the default directions.  This procedure is quick and convenient, but it is important to know the details of the convention used by each frame analysis program, and understand the effect of this convention on the model generated.

As an example, the FEA program Strand7 defines the default principal axes as follows:

The default orientation for Beam2 elements is defined by:
i3 – is the unit vector directed from Node 1 to Node 2.
 i2 – is the unit vector arising from i2 = Z × i3 where Z is the unit vector in the global Z direction
 i1 – completes the right-handed system such that i1 × i2 = i3

This procedure in effect creates an Axis-2 parallel to the XY plane, and an Axis-1 in the plane parallel to the Z axis; i.e. the Z axis is in effect defined as the vertical axis in the model, and the XY plane is horizontal.  It is important to understand how these axes relate to the default axes of standard beam cross sections, and also to understand the effect of using the Y axis as the vertical, rather than the Z.  In the examples below an arch section has been modelled with different assumptions for the axes directions to illustrate the effect on beams that are not parallel to the global axes.  The arch section has been modelled with sections at the base and top using an I beam section to illustrate  the effect of various options on the direction of the web.

The first screen-shot shows the effect of constructing the model with the Y axis as vertical, and no adjustment of the principal axis angles:

Y Axis vertical, no rotation

The arch on the left is parallel to the X axis, and all the beam members are oriented as intended, but as the angle of the arch vertical plane is rotated through 90 degrees, the angle of the principal axes is also rotated, which is not what is required.

Detail at crown, right hand end

Also note that at the right end, the end segment is parallel to the Z axis, and for this one member the beam web is vertical, whereas for the other members lying in the YZ plane, but not parallel to the Z axis, the beam web is horizontal.

Z axis vertical

 For a model with the Z axis vertical the beam Principal Axis-2 is created horizontal (parallel to the XY plane), but in this case the default orientation of the I beam webs, and the rectangular section breadth, is parallel to the Principal Axis-1, which is not what is required in this case.

Also note that the members at the base, which have a longitudinal axis parallel to the Z axis, are rotated relative to the other members.

Z Axis vertical, beams rotated by 90 degrees

Where the Z axis is vertical the correct orientation of the I-beam webs, and the rectangular section breadth, can be obtained by rotating the principal axis through 90 degrees, for all but the vertical beams.

Y Axis vertical, beams rotated by varying amount

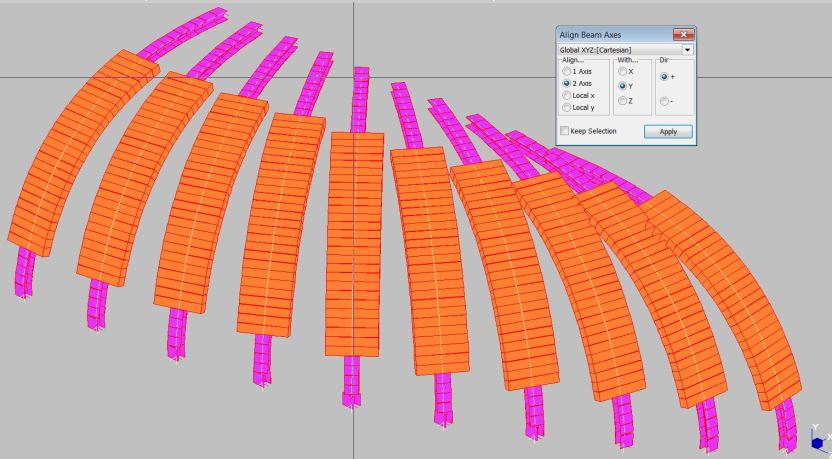
Where the Y axis is vertical each beam segment (other than those in the XY and YZ planes) must be rotated by a different amount.  In Strand7 the Tools-Align-Beam Axes command will perform this task automatically, as illustrated above.

Correction of the orientation of the vertical beams at the base

For both the vertical Y axis and Z axis the beams at the base must be oriented individually, because the Principal Axes 2 are aligned with the Y axis.