Following the previous post, I have updated the py_ConBeamU spreadsheet, and the associated check against Strand7 results.
The new files can be downloaded from:
The download file now includes:
- py_ConBeamU.xlsb: The complete spreadsheet, including examples of all functions
- py_ConBeamU-Check25-2.xlsb: As above, also including the input for all the Strand7 checks
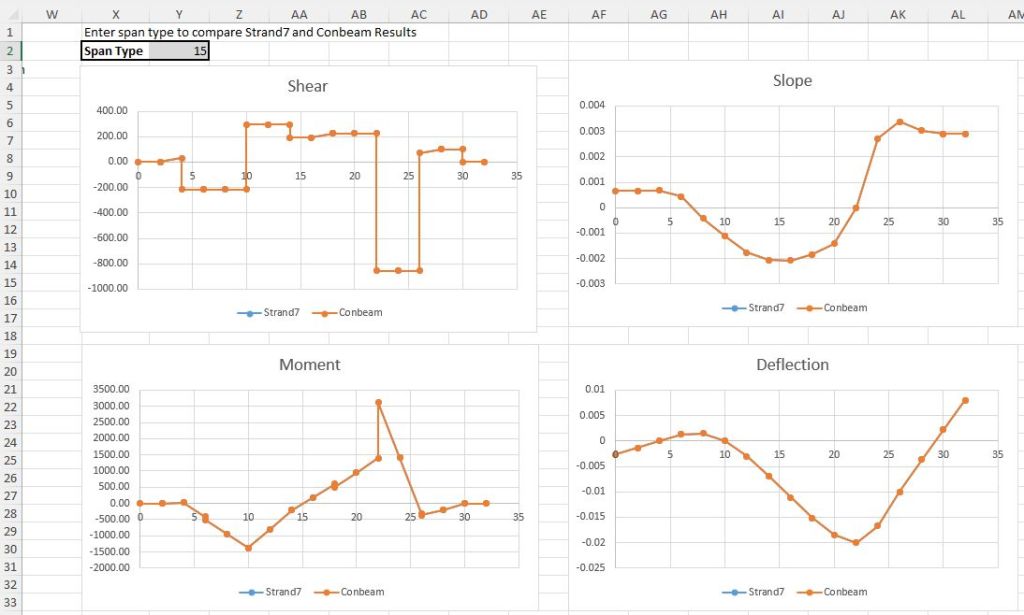
- Check py_ConBeamU-4Dec25.xlsb: Summary of check results, including ConBeam and Strand7 results and graphs for all 90 cases.
- py_ConBeamU-check BeamAct-Dec25.xlsb: Check of BeamAct function against Strand7 results
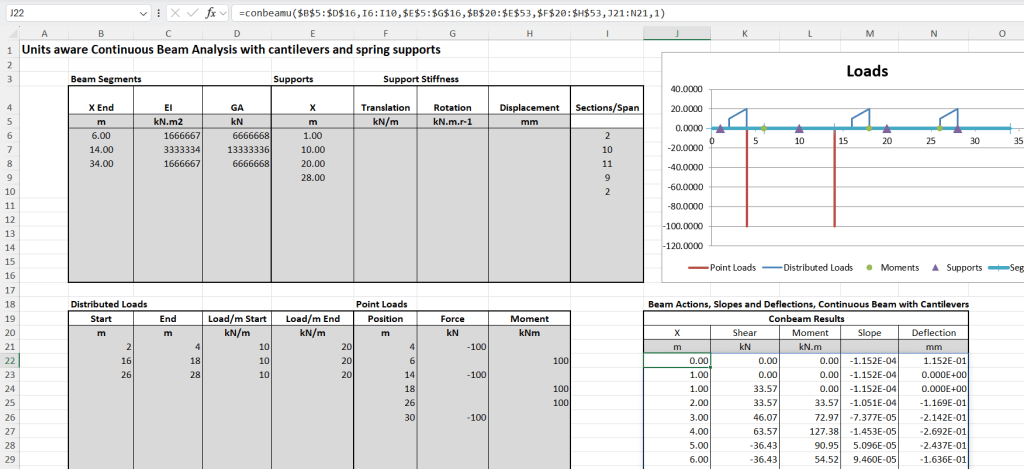
- Beam_Act2.py: The main Python code for the beam analysis functions.
- pyNumpy.py, py_Units4Excel.py, Glob_Loc.py: Required associated Python code
- ConBeam-S7.zip: Strand7 data file and results
For more details of the spreadsheet and included functions see py_ConBeamU and the following associated posts.
Typical results of Strand7 check: