So if there was some guy who had been around since the early seventies singing traditional scottish songs in a modern style, I’d know all about him, right?
But I had never heard of this guy before:
And a full album:

So if there was some guy who had been around since the early seventies singing traditional scottish songs in a modern style, I’d know all about him, right?
But I had never heard of this guy before:
And a full album:
The New Scientist brain twister from last weeks edition has several problems involving pandigital sums, which are additions that use each of the digits from 0 to 9 exactly once, and with no number within the sum that starts with a zero.
The problems can be solved without the use of computers, but it is also interesting to write code to generate brute force solutions, which is what is covered in this post. For anyone who wants to have a go at solving the problems themselves, the screenshot at the bottom of this post contains some solutions, so don’t scroll down.
The problems are:
My Python code and a sample spreadsheet with VBA code can be downloaded from:
I started off with the third problem, using VBA:
Function Pandigital()
Dim a, b, c, d, e, f, g, h, i, j, ResA(1 To 1, 1 To 5), STime
STime = Timer()
For a = 1 To 9
For b = a + 1 To 9
For c = b + 1 To 9
For d = c + 1 To 9
For e = d + 1 To 9
For f = e + 1 To 9
For g = 1 To 9
For h = 0 To 9
For i = 0 To 9
For j = 0 To 9
If (a + b + c + d + e + f + g + h + i + j = 45) Then
If (100 * a + 10 * b + c + 100 * d + 10 * e + f = 1000 * g + 100 * h + 10 * i + j) Then
ResA(1, 1) = 100 * a + 10 * b + c
ResA(1, 2) = 100 * d + 10 * e + f
ResA(1, 3) = ResA(1, 1) + ResA(1, 2)
ResA(1, 4) = 1000 * g + 100 * h + 10 * i + j
ResA(1, 5) = Timer() - STime
Pandigital = ResA
Exit Function
End If
End If
Next j
Next i
Next h
Next g
Next f
Next e
Next d
Next c
Next b
Next a
End Function
This works, and returns the answer in well under a second, but I wanted to avoid so many indented ifs, and also to optimise the code to reduce the number of trials where the values did not meet the stated criteria.
My first effort using Python (linked to Excel with pyxll) was:
@xl_func()
@xl_return('numpy_array')
def py_Pandigital0():
stime = time.perf_counter()
intlist = [0, 1,2,3,4,5,6,7,8,9]
abc = np.array([1,2,3])
def_ = np.array([4,5,6])
facta = np.array([100,10,1])
for k in range(0, 3):
if abc[0] < 4: abc[0] += 1
abc[1] = abc[0]
for l in range(0, 3):
if abc[1] < 5: abc[1] += 1
abc[2] =abc[1]
for m in range(0, 3):
if abc[2] < 6: abc[2] += 1
abcsum = np.dot(abc, facta)
for n in range(0, 3):
if def_[0] < 7: def_[0] += 1
def_[1] = def_[0]
for o in range(0, 3):
if def_[1] < 8: def_[1] += 1
def_[2] = def_[1]
for o in range(0, 3):
if def_[2] < 9: def_[2] += 1
defsum = np.dot(def_, facta)
sum1 = abcsum + defsum
sumlist = intlist.copy()
for p in range(0, 3):
if abc[p] in sumlist:
sumlist.remove(abc[p])
else:
break
if def_[p] in sumlist:
sumlist.remove(def_[p])
else:
break
for q in range(1, 4):
for r in range(0, 4):
for s in range(0, 4):
for t in range(0, 4):
sum2 = sumlist[q]*1000 + sumlist[r]*100 +sumlist[s]*10 + sumlist[t]
if sum1 == sum2:
etime = time.perf_counter() - stime
return np.array([abcsum, defsum, sum1, sum2, etime])
return np.array(sumlist)
The differences from the VBA code are:
The Python code reduced the execution time from 66 milliseconds down to 4 milliseconds.
The Python code was further refined by using the itertools permutations and combinations methods to generate lists of trial groups of digits:
@xl_func()
@xl_arg('in_list', 'numpy_array', ndim=1)
@xl_arg('n', 'int')
@xl_return('numpy_array')
def Perms(in_list, n):
PermA = []
for perm in permutations(in_list,n):
PermA.append(list(perm))
return np.array(PermA)
@xl_func()
@xl_arg('in_list', 'numpy_array', ndim=1)
@xl_arg('n', 'int')
@xl_return('numpy_array')
def Combs(in_list, n):
CombA = []
for comb in combinations(in_list,n):
# if list(comb) == sorted(comb):
CombA.append(list(comb))
return np.array(CombA)
These two functions can also be called from Excel, and return all the combinations or permutations of the specified list from the given input list:
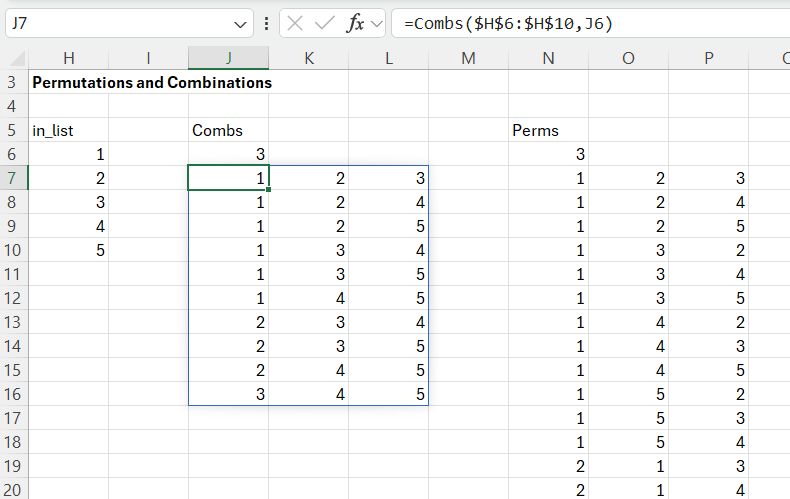
The Combs function returns all the groups of 3 numbers selected from the input list of 5 numbers, listed in the same sequence as in the input array;10 combinations are returned in this case. Note that the code has a commented out line, checking that the returned values are in increasing order. This was suggested by the Bing AI code generator, but was not necessary because the input list was in ascending order.
For more details on permutations and combinations see Combinations and Permutations
The Perms function returns the same 10 groups of numbers, but with each sorted in the 6 possible different orders, returning 60 permutations in all. In my code the Combs function is used to generate the first two numbers, but Perms is used for the final sum because this may be in any order, other than not starting with zero.
@xl_func()
@xl_arg('m', 'int')
@xl_arg('n', 'int')
@xl_return('numpy_array')
def py_Pandigital1(m, n):
stime = time.perf_counter()
intlist = np.array([0,1,2,3,4,5,6,7,8,9])
intlist1 = intlist[2:10-n]
intlist2 = intlist[m+2:]
abcA = Combs(intlist1, m)
defA = Combs(intlist2, n)
rows = abcA.shape[0]
rows2 = defA.shape[0]
o = 10 - (m+n)
facta1 = []
facta2 = []
facta3 = []
for i in range(m-1,-1,-1):
facta1.append(10**i)
facta1 = np.array(facta1)
for i in range(n-1,-1,-1):
facta2.append(10**i)
facta2 = np.array(facta2)
for i in range(o-1,-1,-1):
facta3.append(10**i)
facta3 = np.array(facta3)
for a in range(0, rows):
abc = abcA[a,:]
abcsum = np.dot(abc, facta1)
for b in range(0, rows2):
def_ = defA[b,:]
if def_[0] > abc[-1]:
defsum = np.dot(def_, facta2)
sum1 = abcsum + defsum
sumlist = intlist.copy().tolist()
for c in range(0, m):
if abc[c] in sumlist:
sumlist.remove(abc[c])
else:
break
for c in range(0, n):
if def_[c] in sumlist:
sumlist.remove(def_[c])
else:
break
SumA = Perms(sumlist, 4)
rows3 = SumA.shape[0]
for d in range(0, rows3):
SumA2 = SumA[d, :]
if SumA2[0] == 1: # > 0:
sum2 = np.dot(SumA2, facta3)
if sum1 == sum2:
etime = time.perf_counter() - stime
return np.array([abcsum, defsum, sum1, sum2, etime])
etime = time.perf_counter() - stime
return np.array(etime)
In addition to the use of the combinations and permutations method, this code has also been modified to allow the length of the output numbers to be changed, for instance to check if there was a solution of the form ABCD + EF (there wasn’t). The execution time for this code comes down to 0.8 milliseconds.
For the first two problems the generated values do not need to be in increasing order, but the resulting sum is specified in the input:
@xl_func()
@xl_arg('m', 'int')
@xl_arg('n', 'int')
@xl_arg('sum2', 'int')
@xl_return('numpy_array')
def py_Pandigital2(m, n, sum2):
stime = time.perf_counter()
intlist = [0,1,2,3,4,5,6,7,8,9]
sum2A = np.array([int(d) for d in str(sum2)])
s = sum2A.shape[0]
for i in range(0, s):
intlist.remove(sum2A[i])
abcA = Perms(intlist, m)
defA = Perms(intlist, n)
rows = abcA.shape[0]
rows2 = defA.shape[0]
facta1 = []
facta2 = []
facta3 = []
for i in range(m-1,-1,-1):
facta1.append(10**i)
facta1 = np.array(facta1)
for i in range(n-1,-1,-1):
facta2.append(10**i)
facta2 = np.array(facta2)
for i in range(s-1,-1,-1):
facta3.append(10**i)
facta3 = np.array(facta3)
for a in range(0, rows):
abc = abcA[a,:]
for b in range(0, rows2):
def_ = defA[b,:]
if np.intersect1d(abc, def_).size == 0:
if np.intersect1d(abc, sum2A).size + np.intersect1d(def_, sum2A).size == 0:
abcsum = np.dot(abc, facta1)
defsum = np.dot(def_, facta2)
sum1 = abcsum + defsum
if sum1 == sum2:
etime = time.perf_counter() - stime
return np.array([abcsum, defsum, sum1, sum2, etime])
etime = time.perf_counter() - stime
return np.array(etime)
Changes in this code are:
The reduced time for creating and checking the sum value was more than offset by the options for the first two numbers coming from a permutations list rather than combinations, and the execution time increased to 28 milliseconds.
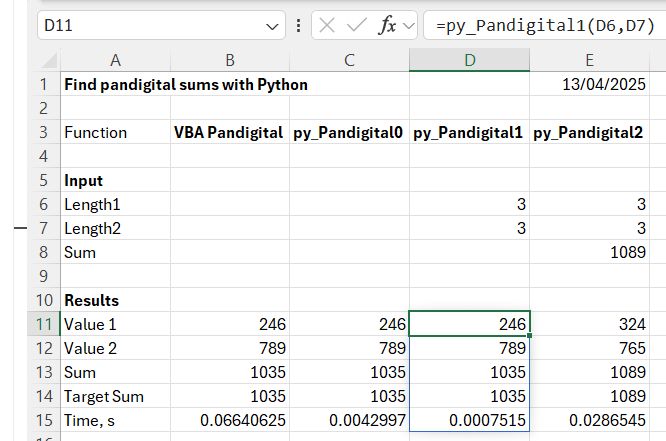
Output results (spoiler alert: includes answers to the problems)
Last Saturday I saw cellist Abel Selaocoe perform with the Australian Chamber Orchestra, performing a mixture of classical works and his own unique compositions. He captured the audience and at the end of the performance received an ovation the like of which I have never seen before.
From his web site: https://www.abelselaocoe.com/
South African cellist Abel Selaocoe is one of the most captivating performers on the world stage today. With an irresistible energy, he has taken the world by storm since bursting onto the scene in 2021 with his BBC Proms debut. Whether with symphony orchestras, in iconic club venues or at major mainstream festivals, Abel combines virtuosic cello and vocal performance with improvisation and sweeps audiences along in captivating shows which blaze with creation, sending audiences home on a high.
Abel grew up in Sebokeng, where he first began learning cello with his brother at the African Cultural Organisation of South Africa (ACOSA) in Soweto. Abel’s affinity for the cello became quickly apparent and he continued his studies on scholarship at St John’s College before moving to the UK where he found a musical home at the Royal Northern College of Music in Manchester. In Manchester, he met the musicians who are now his most regular collaborators, and this has led to the formation of his bands, Chesaba and the Bantu Ensemble.
My Blogroll (bottom of the right-hand column) is badly in need of updating, but the link below has a list of 60 currently active Excel blogs and websites:
60 Best Excel Blogs and Websites in 2025
Those at the top of the list include several long running but still active sites, as well as several that I had not heard of before.
And scrolling down to number 26 we find none other than Newton Excel Bach 🙂
I have just uploaded a new version ULS Design Functions-biax, which can be downloaded (together with the uni-axial version) from:
The main changes are added code parameters from Eurocode 2:
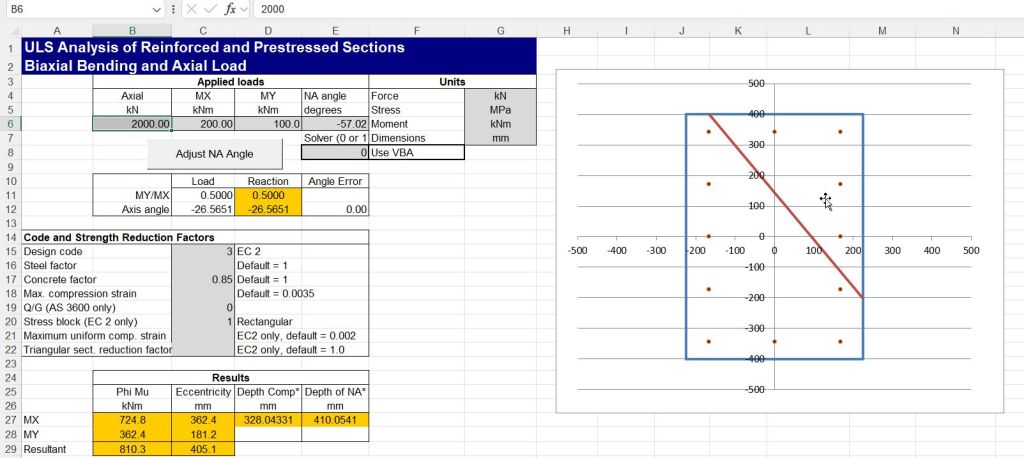
Detailed output for a specified load and neutral axis angle is as in previous versions:
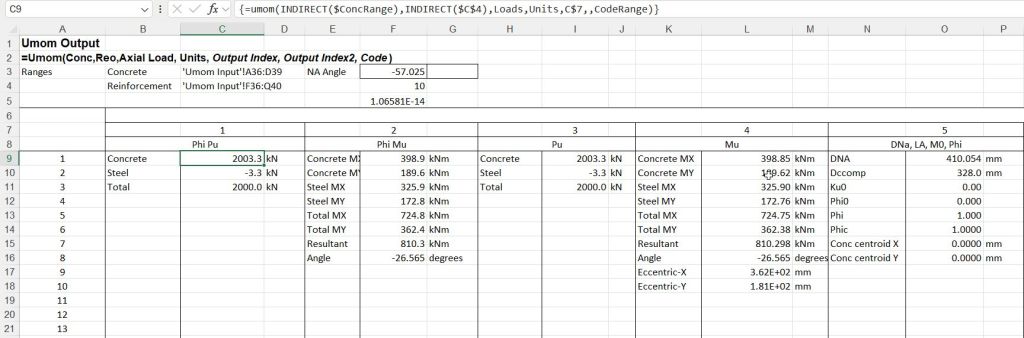
There are also functions that will generate various interaction diagrams:
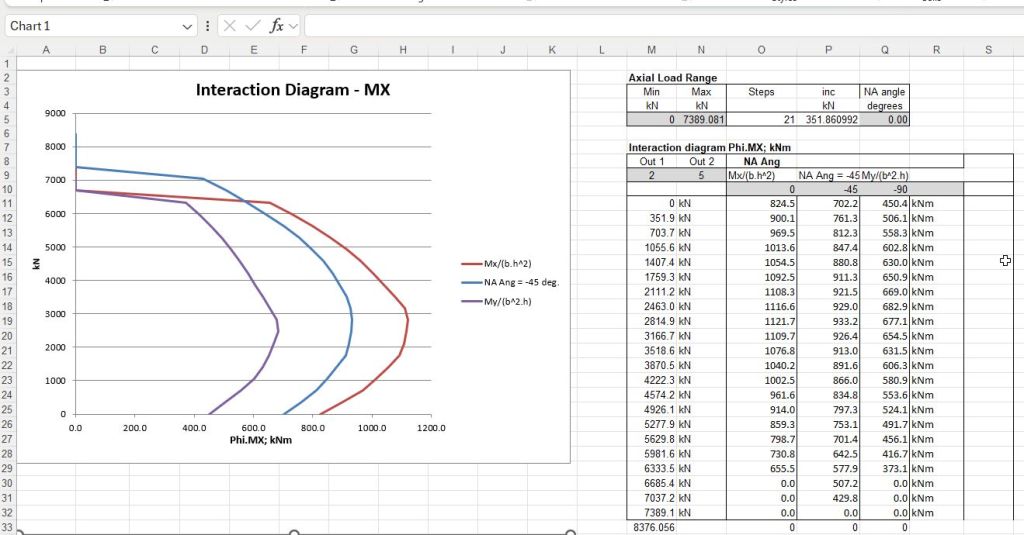

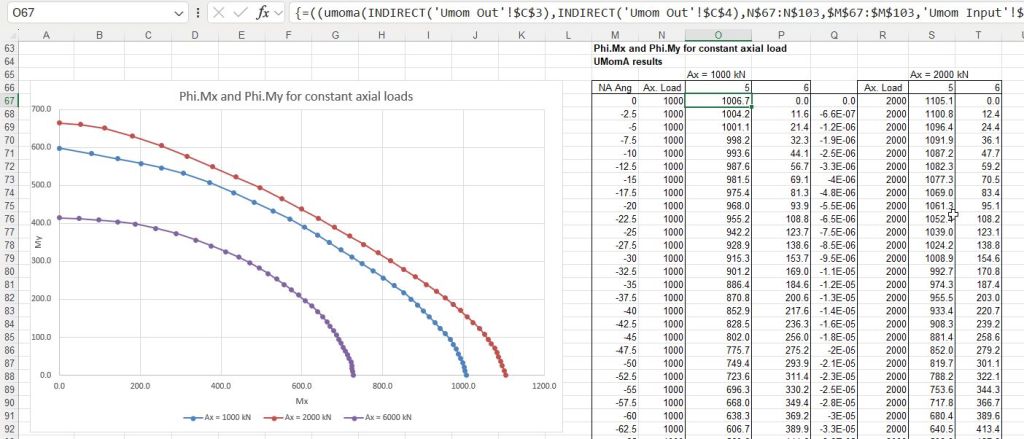
For more details and examples see: Biaxial Bending Update.