Newton Excel Bach, not (just) an Excel Blog

This post looks at some of the options for generating random numbers in Excel and Python. The code and example spreadsheets can be downloaded from:

Updated Numpy files at: py_SciPy.zip
Code added to the Pandigital files at: Pandigitals.zip

The py_SciPy download contains full open-source Python code and example spreadsheets for a wide range of Scipy functions, as well as the Numpy functions covered in this post. For more details, see the series of posts starting at: Scipy functions with Excel and pyxll. Also see Python and pyxll for details of the pyxll add-in, required to link my Python code to Excel.

The code below calls functions from the Python random or secret modules:

@xl_func(category="py-Maths", help_topic="https://docs.python.org/3/library/random.html#functions-for-integers!0")
@xl_arg('start', 'int')
@xl_arg('stop', 'int')
def py_RandBetween(start, stop):
    return randint(start, stop)

@xl_func(category="py-Maths", help_topic="https://docs.python.org/3/library/random.html#functions-for-integers!0")
@xl_arg('start', 'int')
@xl_arg('stop', 'int')
@xl_arg('step', 'int')
def py_RandRange(start, stop, step=1):
    return randrange(start, stop, step)

@xl_func(category="py-Maths", help_topic="https://docs.python.org/3/library/secrets.html#random-numbers!0")
@xl_arg('start', 'int')
@xl_arg('stop', 'int')
def py_RandBelow(stop):
    return randbelow(stop)

Function results are shown in the screenshot below, together with three Numpy functions and the Excel built-in Randbetween and Randarray functions:

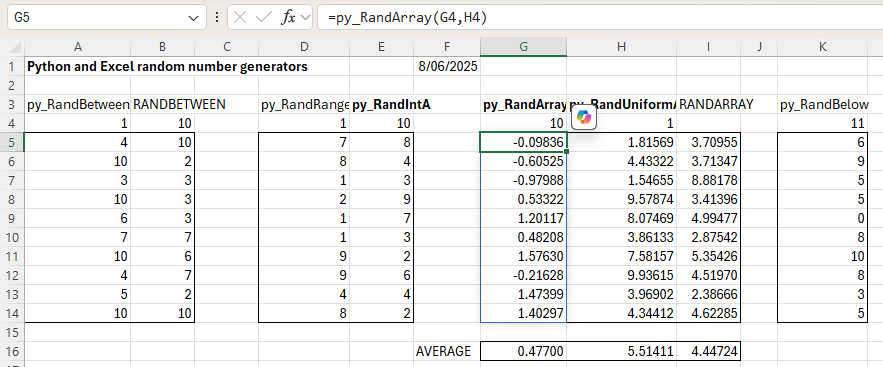
• py_RandBetween and Excel Randbetween operate in the same way, returning a single integer, between the specified inclusive limits.
• py_RandRange and py_RandIntA operate in a similar way, returning integers between the lower limit and below the upper limit. py_RandRange also has a step input (default = 1), and returns only integers with the specified step interval above the minimum value. py_RandIntA is a Numpy function, and returns an array with the specified number of rows and (optionally) columns.
• py_RandArray and py_RandUniform are Numpy functions and also return arrays with multiple rows and 1 or more columns. py_RandArray returns a normal distribution with zero mean and 1.0 variance. py_RandUniformA operates in a similar way to the Excel Randarray function, returning an array of floats of the specified size with uniform distribution over the specified range.
• py_RandBelow returns an integer between zero and 1 less than the upper limit. It is part of the Python random.secrets module and provides greater security in the generation of random integers.

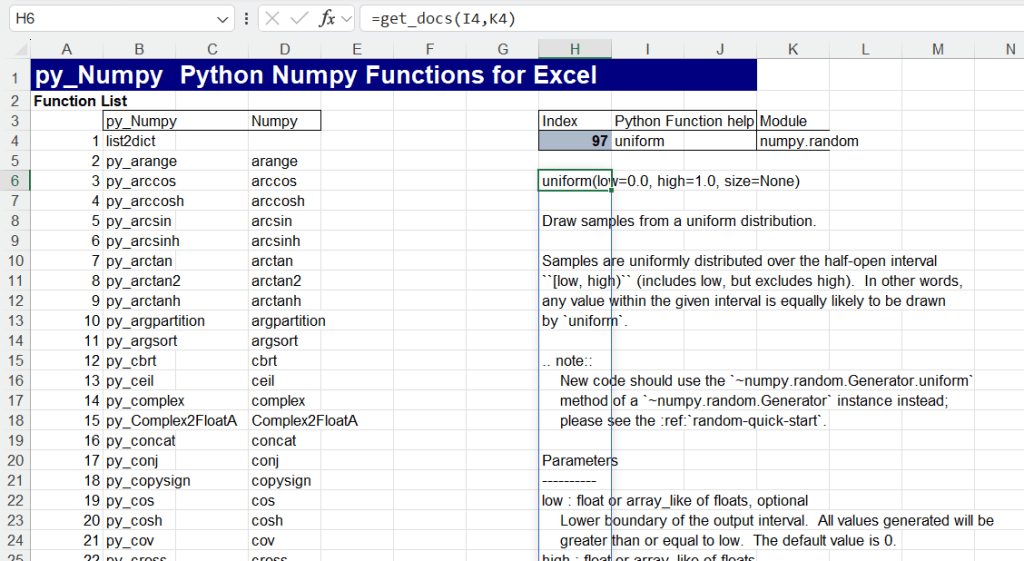
All the Python and Numpy functions provide direct access to the on-line Python help by clicking the “help on this function” link in the function dialogue:

The help is also available as text within Excel for the Numpy functions, using the py_Numpy spreadsheet:

The code below generates arrays of numerical “palindromes”, i.e. integers with the same value when read from right to left:

@xl_func()
@xl_arg('start', 'int')
@xl_arg('stop', 'int')
def PalindromeNum(start, stop):
    stime = time.perf_counter()
    palindromes = []
    for num in range(start, stop):
        if str(num) == str(num)[::-1]:
            palindromes.append(num)
    palindromes.insert(0, len(palindromes))
    palindromes.insert(0, time.perf_counter() - stime)
    return palindromes

@xl_func()
def PalindromeNum8():
    stime = time.perf_counter()
    palindromes = []
    for one in range(1, 10):
        for two in range(0, 10):
            for three in range(0, 10):
                for four in range(0, 10):
                    palindromes.append(int(f'{one}{two}{three}{four}{four}{three}{two}{one}'))
    palindromes.insert(0, len(palindromes))
    palindromes.insert(0, time.perf_counter() - stime)
    return palindromes

The code is based on this Quora post: How many 6 digit palindrome numbers can be formed?

The functions return an array of all the palindromes between the specified limits (for the PalindromeNum function, or between 10,000,000 and 100,000,000 for PalindromeNum8. The functions also return the execution time and the number of palindromes found.

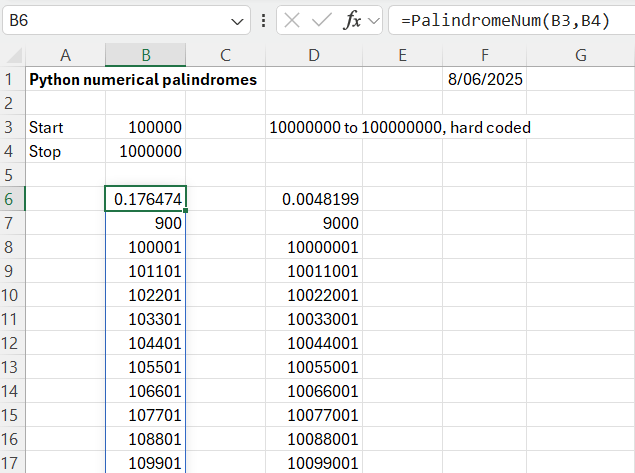
The PalindromeNum function works by generating all the integers in the specified range, then checking if they are palindromes, by comparing a string of each value with the reversed string. This works reasonably quickly for up to 1 million values, but rapidly slows down for bigger ranges:

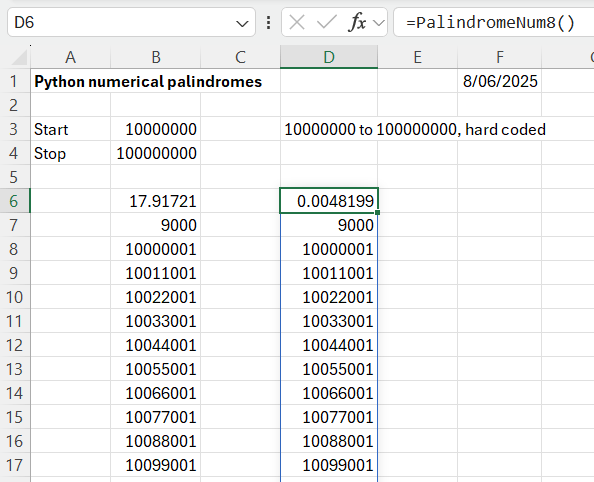
The PalindromeNum8 function works by generating all the possible integers of half the required size, then appending the reversed value as a string, and converting the result back to an integer. For the example shown this is about 3500 times faster than the original code! The problem with the faster code is that it needs a variable number of nested loops, depending on the magnitude of the integers, so the code would need reworking to allow ranges of different magnitude. Since the purpose of the exercise is to display Python techniques for manipulating lists and strings, I will leave that as an exercise for the reader!